Triangular Prism
A prism is a solid figure with flat faces, two identical bases, and with the same cross-section all along its length. The name of a particular prism depends on the two bases of the prism which can be triangles, rectangles, or any polygon. For example, a prism with triangular bases is called a triangular prism and a prism with a square base is called a square prism, and so on. A triangular prism has two triangular bases and three rectangular lateral faces. Let us learn more about the triangular prism in this article.
| 1. | What is a Triangular Prism? |
| 2. | Triangular Prism Faces Edges Vertices |
| 3. | Triangular Prism Net |
| 4. | Triangular Prism Formulas |
| 5. | FAQs on Triangular Prism |
What is a Triangular Prism?
A triangular prism is a 3D shape with two identical faces in the shape of a triangle connected by three rectangular faces. The rectangular faces are referred to as the lateral faces, while the triangular faces are called bases. The bases are also called the top and the bottom (faces) of the prism.
Triangular Prism Meaning: A triangular prism is a 3D polyhedron with three rectangular faces and two triangular faces. The 2 triangular faces are congruent to each other, and the 3 lateral faces which are in the shape of rectangles are also congruent to each other. Thus, a triangular prism has 5 faces, 9 edges, and 6 vertices. Observe the following image of a triangular prism in which l represents the length of the prism, h represents the height of the base triangle, and b represents the bottom edge of the base triangle.
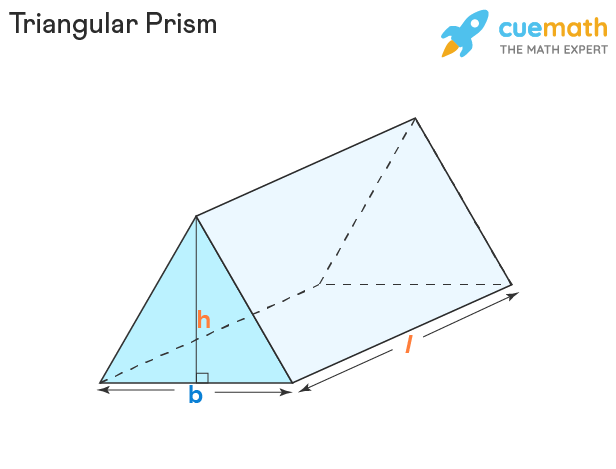
Triangular Prism Properties
The properties of a triangular prism help us to identify it easily. Listed below are a few properties of a triangular prism:
- A triangular prism has 5 faces, 9 edges, and 6 vertices.
- It is a polyhedron with 3 rectangular faces and 2 triangular faces.
- The two triangular bases are congruent to each other.
- Any cross-section of a triangular prism is in the shape of a triangle.
Right Triangular Prism
A right triangular prism is a prism in which the triangular faces are perpendicular to the three rectangular faces. In other words, the angle formed at the intersection of triangle and rectangle faces should be 90 degrees, therefore, the triangular faces are perpendicular to the lateral rectangular faces. A right triangular prism has 6 vertices, 9 edges, and 5 faces.
Triangular Prism Faces Edges Vertices
As mentioned above, a triangular prism has 5 faces including 3 lateral rectangular faces and 2 triangular bases, 9 edges, and 6 vertices. The vertices of the triangular prism are the vertices of the two triangular bases connected by lines that form rectangles. Its edges include 6 edges of two triangular bases (3 + 3) and 3 sides that join the bases.
| Faces | Edges | Vertices | |
|---|---|---|---|
| Triangular Prism | 5 | 9 | 6 |
Triangular Prism Net
The net of a triangular prism is a pattern that is seen when the surface of the prism is opened, flattened, and laid out such that all the faces are seen clearly. It is two-dimensional. This net can be folded up to make a triangular prism. It shows that the bases of the prism are shaped in a triangle and the lateral faces are shaped like a rectangle. The figure given below shows the net of a triangular prism where the triangles and the rectangles are seen clearly.
Triangular Prism Formulas
There are two important formulae of a triangular prism which are surface area and volume. A brief explanation of both is given below along with the formula.
Surface Area of a Triangular Prism
The surface area of a triangular prism is the area that is occupied by its surface. It is the sum of the areas of all the faces of the prism. Hence, the formula to calculate the surface area is:
Surface area = (Perimeter of the base × Length) + (2 × Base Area) = (a + b + c)L + bh
where,
- b is the bottom edge of the base triangle,
- h is the height of the base triangle,
- L is the length of the prism,
- a, b, and c are the three edges (sides) of the base triangle
- (bh) is the combined area of the two triangular faces, because [2 × (1/2 × bh)] = bh.
For more information on the surface area formula and calculations, check the article on the surface area of a triangular prism.
Volume of a Triangular Prism
The volume of a triangular prism is the product of its triangular base area and the length of the prism. As we already know that the triangular prism base is in the shape of a triangle, the area of the base will be the same as that of a triangle. Hence, the Volume of a Triangular Prism = area of base triangle × length or it can also be written as Volume of Triangular Prism = ½ × b × h × l, where b is the base length of the triangle, h is the height of the triangle, and l is the length of the prism.
► Related Topics
Listed below are a few interesting topics that are related to the triangular prism in geometry.
FAQs on Triangular Prism
What is a Triangular Prism?
A triangular prism is a three-dimensional polyhedron, made up of two triangular faces and three rectangular faces. It has 5 faces, 9 edges, and 6 vertices. The 2 bases are in the shape of a triangle and the other 3 faces are shaped like a rectangle. Some real-life examples of a triangular prism are camping tents, chocolate candy bars, rooftops, etc.
What is the Volume of a Triangular Prism?
The volume of a triangular prism is the three-dimensional space enclosed by it. It is the product of its triangular base area and its length. The formula to find the volume is, Volume of a Triangular Prism = area of base triangle × length, or it can also be written as ½ × b × h × l, where b is the base length of the triangle, h is the height of the triangle, and l is the length between the triangular bases. The volume of a triangular prism is expressed in cubic units such as in3.
What is the Surface Area of a Triangular Prism?
The surface area of a triangular prism is the total area that is occupied by its surface. The formula to find the surface area of a triangular prism is (Perimeter of the base × Length) + (2 × Base Area) square units.
How many Vertices and Edges does a Triangular Prism have?
A triangular prism consists of 6 vertices and 9 edges. The edges are also known as the sides and the vertices are known as the corners of the prism. It has 5 faces of which 2 are triangular faces and 3 are rectangular faces.
What is a Right Triangular Prism?
A right triangular prism is a prism in which the angle formed between the edges of triangular bases and edges of the rectangular faces is 90 degrees. Other properties of triangular prism remain the same.
How many Faces does a Triangular Prism have?
A triangular prism has 5 faces of which 3 are lateral rectangular faces and 2 are triangular faces which form the top and the bottom bases of the prism.
How many Sides does a Triangular Prism have?
A triangular prism has 9 sides in all. These sides are also called the edges of the prism.
What is the Difference between a Triangular Prism and a Rectangular Prism?
The main difference between a triangular prism and a rectangular prism is that the bases of a triangular prism are triangles, while the bases of a rectangular prism are rectangles. Apart from this, a rectangular prism has 6 faces and 12 edges, while a triangular prism has 5 faces and 9 edges.
Is a Pyramid a Triangular Prism?
No, a pyramid is not a triangular prism. A triangular pyramid is a solid shape with 4 triangular faces with a central vertex point. Whereas a triangular prism is a polyhedron with 2 congruent triangular bases and the remaining are rectangular faces. A triangular prism is a 3D polyhedron with triangle-shaped bases and rectangle-shaped lateral faces. Hence, a pyramid is not a triangular prism.