Volume of Right Circular Cone
The volume of a right circular cone is the space occupied by the right circular cone or the capacity of the right circular cone. A right circular cone is a three-dimensional solid object which is having a circle at one end and a pointed end on the other. The pointed end is also known as the vertex of the cone. A right circular cone is a cone whose axis is perpendicular to the plane of the base. A right circular cone is generated by a revolving right triangle about one of its legs. In this section, we will learn about the volume of the right circular cone along with a few solved examples and practice questions.
| 1. | What is the Volume of Right Circular Cone? |
| 2. | Volume of Right Circular Cone Formula |
| 3. | How to Calculate Volume of Right Circular Cone? |
| 4. | FAQs on Volume of Right Circular Cone |
What is the Volume of Right Circular Cone?
The volume (V) of a right circular cone can be defined as the space occupied by the right circular cone. The volume of the right circular cone is equal to one-third of the product of the area of the circular base and its height. The formula for the volume is V = (1/3) × πr2h where r is the radius of the base circle and h is the height of the cone. If we correlate the volume of the cylinder and the right circular cone, the volume of the right circular cone is one-third of the volume of the cylinder of the same radius and height. The volume of the right circular cone = (1/3) × volume of a cylinder. As we know right circular cone is a three-dimensional shape, thus, the volume of the right circular cone is also in a three-dimensional plane. The unit of the right circular cone is given in terms of cm3, m3, in3, or ft3, etc.
We can see that from the image shown below.
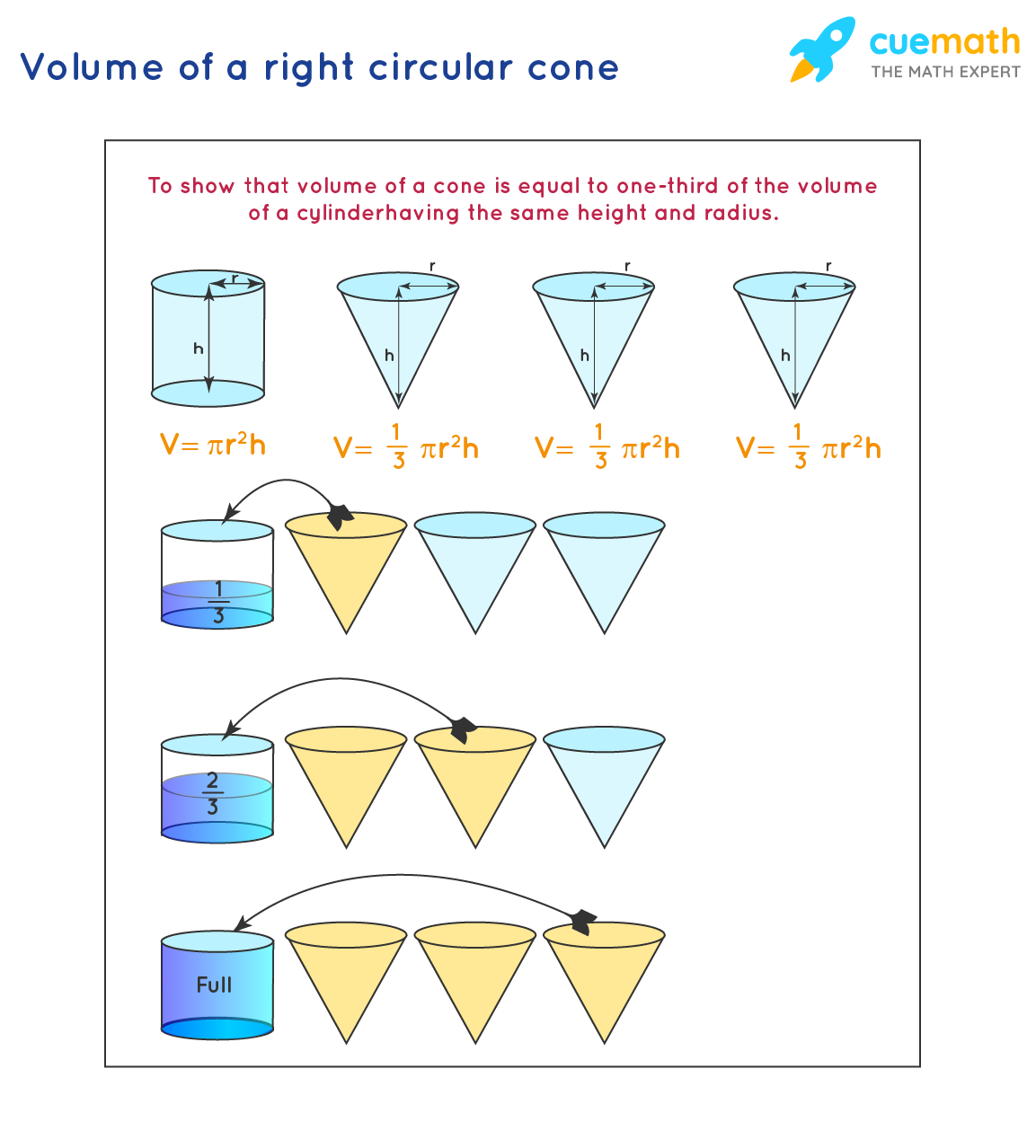
Volume of Right Circular Cone Formula
The volume of the cone is equal to one-third of the product of the area of the base and its height. The base area of the cone is obtained by multiplying the square of its radius to π. Thus, the formula for the volume of the right circular cone, with a radius r and height h is "(1/3)πr2h".
How to Calculate Volume of Right Circular Cone?
The volume of the right circular cone is equal to (1/3)πr2h". By following the steps mentioned below we can find the volume of a right circular cone.
- Step 1: Calculate the radius of the base and height of the right circular cone.
- Step 2: Find the square of the radius.
- Step 3: Find out the product of the square of its radius to π. This will give the area of the circular base of the right circular cone.
- Step 4: Multiply the result with the height of the right circular cone.
- Step 5: Multiply the result thus obtained with 1/3.
- Step 6: Represent the answer in cubic units.
Example: Find the volume of the right circular cone having a radius of 3 units and a height of 7 units. (Use π = 22/7)
Solution: Given that r = 3 units and h = 7 units
As we know, volume of right circular cone, V = (1/3)πr2h
⇒ V = (1/3) × (22/7) × (32) × 7
⇒ V = 66 cubic units
Therefore, the volume of the right circular cone is 66 cubic units.
Solved Examples on Volume of Right Circular Cone
-
Example 1: The radius of a right circular cone is 5 in. Find the volume of the right circular cone if the height is 15 in.
Solution: Given the length of the radius, r = 5 in and height of the cone, h = 15 in.
Using the formula for the volume of the right circular cone we get,
V = (1/3)πr2h
⇒ V = (1/3) π × 52 × 15
⇒ V = π × 52 × 5
⇒ V = 392.7Therefore, the volume of the right circular cone is 392.7 cubic inches.
-
Example 2: Emanuel has given the volume of the right circular cone as 244π cubic units. Find the radius of the circular base of the cone if the height of the cone is 183 units.
Solution: Given the volume of the right circular cone, V = 244π, and height of the cone, h = 183
Using the formula for the volume of the right circular cone,
V = (1/3)πr2h
⇒ 244π = (1/3) π × r2× 183
⇒ 4 = r2
⇒ r = 2So, the radius of the cone is 2 units.

FAQs on Volume of Right Circular Cone
What is the Volume of the Right Circular Cone?
The volume of a right circular cone is the amount of space occupied by it. A right circular cone is one whose axis is perpendicular to the plane of the base. A right circular cone is generated by revolving a right triangle about one of its legs. The volume of the right circular cone is given in cubic units where units can be centimeters, meters, inches, or feet.
What is the Volume of a Right Circular Cone Formula?
The formula to determine the value of the volume of a right circular cone is given as V = (1/3)πr2h, where "V", "r" and "h" are the volume, radius, and h is the height of the cone. This formula shows the dependence of the volume of the cone on the radius and height of the cone directly.
How to Find the Volume of a Right Circular Cone?
We can determine the volume of a right circular cone using the following steps:
- Step 1: Identify the radius of the base of the cone and the height of the cone.
- Step 2: Determine the square of the radius.
- Step 3: Multiply the square of its radius to π. (This gives the area of the circular base of the cone).
- Step 4: Now, find the product of the result with the height of the cone.
- Step 5: Divide the obtained answer by 3.
- Step 6: Represent the obtained answer in cubic units.
How to Find the Height of the Right Circular Cone If the Volume of Right Circular Cone is Given?
We can find the height of the right circular cone if the volume of the right circular cone is given using the below steps:
- Step 1: Identify the given dimensions of the right circular cone and let the height of the right circular cone is "h"
- Step 2: Find the square of the radius and multiply it by π.
- Step 3: Now, find the product of the result with the height of the cone, "h".
- Step 4: Divide the obtained answer by 3 and solve for "h".
- Step 5: Once the equation is solved for "h", represent the obtained answer in units.
What is the Formula of Volume of Right Circular Cone In Terms of Slant Height?
The formula of volume of the right circular cone in terms of slant height is given by using the relation between l = √(r2 + h2) using the Pythagoras theorem. Thus, the volume of the right circular cone in terms of slant height is V = (1/3)πr2h = (1/3)πr2√(l2−r2).
What Happens to the Volume of Right Circular Cone If the Radius of the Cone is Doubled?
The volume of the right circular cone is quadrupled if the radius of the cone is doubled as "r" in the formula of volume of the right circular cone will be substituted by "2r", giving the formula, V = (1/3)π(2r)2h = 4 ((1/3)πr2h) which is four times the original volume of the right circular cone.
What Happens to the Volume of Right Circular Cone If the Height of the Cone is Halved?
The volume of the right circular cone is halved if the height of the cone is halved as "h" in the formula of volume of the right circular cone will be substituted by "h/2", giving the formula, V = (1/3)πr2(h/2) = (1/2) × (1/3)πr2h which is half the original volume of the right circular cone.
visual curriculum