A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
Solution:
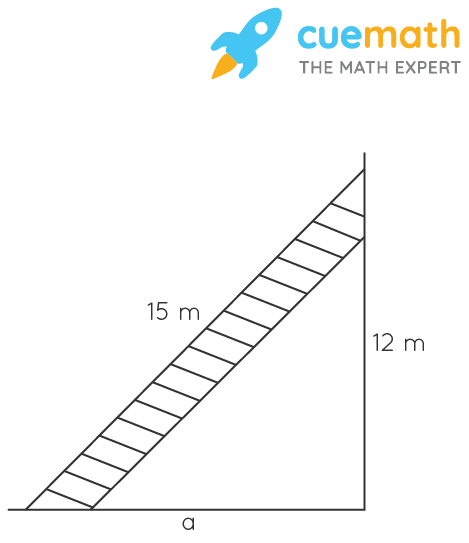
This question is based on the concept of the right-angled triangle. Let's visualize it as shown below.

As it is clear from the figure that the ladder is kept slanted on the wall.
Hence, consider the length of the ladder as hypotenuse that is AB = 15m and as it is kept slanted on the wall so, we consider the wall as perpendicular that is AC = 12 m.
Now, we must find out the distance of the foot of the ladder from the wall that is BC = a.
Now by applying the Pythagoras theorem in triangle ABC, we can find out BC.
Given, Length of ladder AB = 15 m, Length of wall AC = 12 m
According to Pythagoras theorem,
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
(AB)2 = (AC)2 + (BC)2
(15)2 = (12)2 + (a)2
225 = 144 + (a)2
225 - 144 = (a)2
81 = a2
a = 9 m
Therefore, the distance of the foot of the ladder from the wall is 9 m.
☛ Check: NCERT Solutions for Class 7 Maths Chapter 6
Video Solution:
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5 Question 3
Summary:
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. The distance of the foot of the ladder from the wall is 9 m.
☛ Related Questions:
- A Tree Is Broken At A Height Of 5 M From The Ground And Its Top Touches The Ground At 12 M From The Base Of The Tree Find The Original Height Of The Tree
- Angles Q And R Of A Pqr Are 25o And 65o Write Which Of The Following Is True Ipq2 Qr2 Rp2 Iipq2 Rp2 Qr2 Iiirp2 Qr2 Pq2
- Find The Perimeter Of The Rectangle Whose Length Is 40 Cm And A Diagonal Is 41 Cm
- The Diagonals Of A Rhombus Measure 16 Cm And 30 Cm Find Its Perimeter
visual curriculum