ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD

Solution:

We will use the following concepts to answer the question:

• A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle.

• The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.

• The sum of angles in a triangle is 180°.

• Angles in the same segment are equal.

Based on the data given, let's draw the figure as shown below.

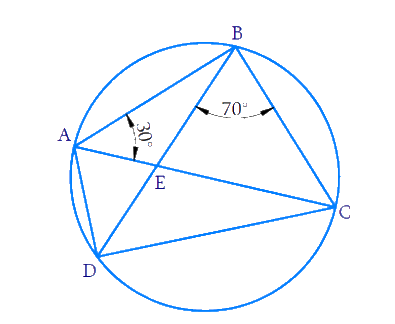
In the triangles, ABD and BCD, ∠CAD = ∠CBD = 70°. (Angles in the same segment are equal)

Hence, ∠BAD = ∠CAB + ∠DAC

= 30° + 70°  = 100°

Thus, ∠BAD = 100°

Since ABCD is a cyclic quadrilateral, the sum of either pair of opposite angles of a cyclic quadrilateral is 180º.

∠BAD + ∠BCD = 180°

∠BCD = 180° - 100°

= 80°

Thus, ∠BCD = 80°

Also given AB = BC.

So, ∠BCA = ∠BAC = 30° (Base angles of isosceles triangle are equal)

∠ECD = ∠BCD - ∠BCA

= 80° - 30°

= 50°

Thus, ∠ECD = 50°

☛ Check: Class 9 Maths NCERT Solutions Chapter 10

---

Video Solution:

ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD

Maths NCERT Solutions Class 9 Chapter 10 Exercise 10.5 Question 6

Summary:

If ABCD is a cyclic quadrilateral whose diagonals intersect at a point E, ∠DBC = 70°, ∠BAC = 30°, and AB = BC, then ∠BCD = 80° and ∠ECD = 50°.

---

☛ Related Questions:

• If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
• If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
• Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D, P and Q respectively (see Fig. 10.40). Prove that ∠ACP = ∠QCD.
• If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.