If the non-parallel sides of a trapezium are equal, prove that it is cyclic

Solution:

We know that, if the sum of a pair of opposite angles of a quadrilateral is 180°, the quadrilateral is cyclic. 

Draw a trapezium ABCD with AB || CD

AD and BC are the non-parallel sides that are equal. AD = BC. Draw AM ⊥ CD and BN ⊥ CD.

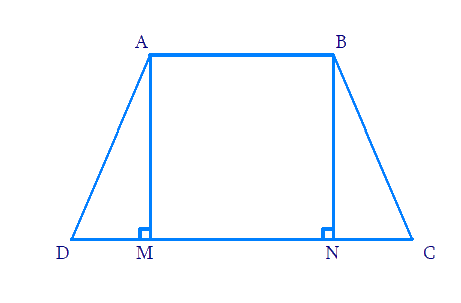
Consider ΔAMD and ΔBNC

AD = BC (Given)

∠AMD = ∠BNC (90°)

AM = BN (Perpendicular distance between two parallel lines is same)

By RHS congruence, ΔAMD ≅ ΔBNC.

Using CPCT, ∠ADC = ∠BCD.....(1)

∠BAD and ∠ADC are on the same side of transversal AD.

∠BAD + ∠ADC = 180°

∠BAD + ∠BCD = 180° [From equation(1)]

This equation proves that the sum of opposite angles is supplementary. Hence, ABCD is a cyclic quadrilateral.

☛ Check: NCERT Solutions Class 9 Maths Chapter 10

Video Solution:

If the non-parallel sides of a trapezium are equal, prove that it is cyclic

Maths NCERT Solutions Class 9 Chapter 10 Exercise 10.5 Question 8

Summary:

If the non-parallel sides of a trapezium are equal, then it is a cyclic quadrilateral

☛ Related Questions:

• Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D, P and Q respectively (see Fig. 10.40). Prove that ∠ACP = ∠QCD.
• If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
• ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD
• Prove that a cyclic parallelogram is a rectangle.