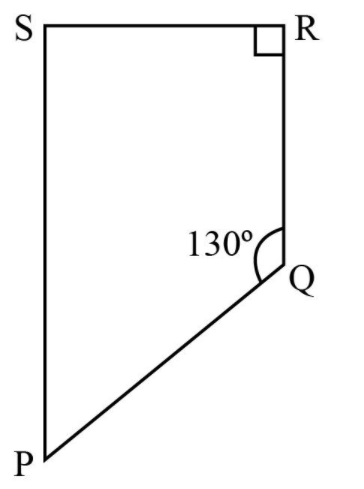
Find the measure of ∠P and ∠S if SP || RQ in Fig 3.34. (If you find m∠R , is there more than one method to find m∠P?)
Solution:
Given SP is parallel to RQ and SR is the traversal drawn to these lines. Hence, SPQR is a trapezium.
∠S + ∠R = 180°
∠S + 90° = 180° [Since, ∠R = 90° in the given figure]
∠S = 180° - 90°
∠S = 90°
Using the angle sum property of a quadrilateral,
∠S + ∠P + ∠Q + ∠R = 360°
90° + ∠P + 130° + 90° = 360°
∠P + 310° = 360°
∠P = 360° - 310°
∠P = 50°
Alternate Method:
∠P + ∠Q = 180° (adjacent angles with SP || RQ )
∠P + 130° = 180°
∠P = 180° - 130°
∠P = 50°
Also,
∠S + ∠R = 180° (adjacent angles)
∠S + 90° = 180°
∠S = 180° - 90°
∠S = 90°
☛ Check: Class 8 Maths NCERT Solutions Chapter 3
Video Solution:
Find the measure of ∠P and ∠S if SP is parallel to RQ in the below figure. (If you find m∠R , is there more than one method to find m∠P?)
NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.3 Question 12
Summary:
The measure of ∠P and ∠S if SP is parallel to RQ in the below figure is ∠S = 90° and ∠P = 50°.
☛ Related Questions:
- The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
- The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
- In the above figure both RISK and CLUE are parallelograms. Find the value of x.
- Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
visual curriculum