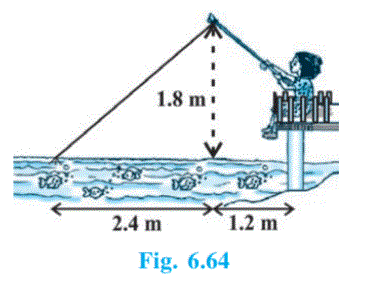
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. 6.64)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
Solution:
Using Pythagoras Theorem to find AB and ED
BD = 3.6 m, BC = 2.4 m, CD = 1.2 m
AC = 1.8 cm
In ΔACB
AB² = AC² + BC²
= (1.8)² + (2.4)²
= 3.24 + 5.76
AB² = 9
AB = 3
Length of the string out AB = 3cm
Let the fly at E after 12 seconds
String pulled in 12 seconds = 12 × 5
= 60 cm
=0.6 m
AE = 3m - 0.6 m
= 2.4 m
Now In
ΔACE
CE2 = AE² - AC²
= (2.4)² - (1.8)²
CE² = 5.76 - 3.24
= 2.5²
CE = 1.587 m
DE = CE + CD
= 1.587 + 1.2
= 2.787
DE = 2.79 m
The horizontal distance of the fly after 12 seconds = 2.79 m
☛ Check: NCERT Solutions for Class 10 Maths Chapter 6
Video Solution:
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. 6.64)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.6 Question 10
Summary:
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. If she pulls in the string at the rate of 5 cm per second, then the horizontal distance of the fly after 12 seconds = 2.79 m
☛ Related Questions:
- In Fig. 6.56, PS is the bisector of ∠QPR of ΔPQR. Prove that QS/SR = PQ/PR.
- In Fig. 6.57, D is a point on hypotenuse AC of ΔABC , such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that: (i) DM² = DN.MC (ii) DN² = DM.AN.
- In Fig. 6.58, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that: AC² = AB² + BC² + 2BC.BD.
- In Fig. 6.59, ABC is a triangle in which ∠ABC less than 90° and AD ⊥ BC. Prove that: AC² = AB² + BC² - 2BC × BD.
visual curriculum