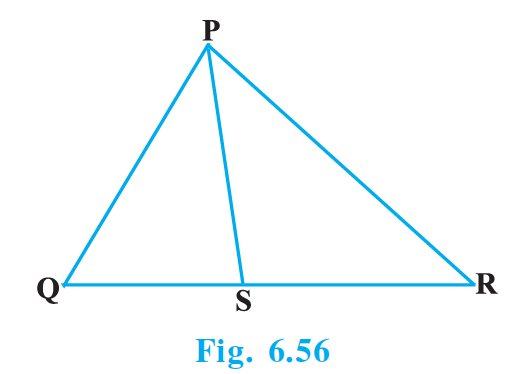
In Fig. 6.56, PS is the bisector of ∠QPR of ΔPQR. Prove that QS/SR = PQ/PR

Solution:

According to Basic Proportionality Theorem, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Draw a line parallel to PS, through R, which intersects QP produced at T.

From the figure, PS || RT

In ΔQPR

∠QPS = ∠SPR (Since PS is the bisector of ∠QPR) ...... (i)

But, ∠PRT = ∠SPR (alternate interior angles)...... (ii)

∠QPS = ∠PTR (Corresponding angles)..... (iii)

From equations (i), (ii), and (iii)

∠PTR = ∠PRT

Thus, PR = PT (Since in a triangle sides opposite to equal angles are equal) ....... (iv)

In ΔQRT, PS || RT

QS/SR = QP/PT (Basic Proportionality Theorem)

Thus, QS/SR = QP/PR [From (iv)]

☛ Check: NCERT Solutions for Class 10 Maths Chapter 6

Video Solution:

In Fig. 6.56, PS is the bisector of ∠QPR of ΔPQR. Prove that QS/SR = PQ/PR

NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.6 Question 1

Summary:

In the given figure, PS is the bisector of ∠QPR of ΔPQR. Hence we have proved that QS/SR = PQ/PR.

☛ Related Questions:

• In Fig. 6.57, D is a point on hypotenuse AC of ΔABC , such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that: (i) DM² = DN.MC (ii) DN² = DM.AN.
• In Fig. 6.58, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that: AC² = AB² + BC² + 2BC.BD.
• In Fig. 6.59, ABC is a triangle in which ∠ABC less than 90° and AD ⊥ BC. Prove that: AC² = AB² + BC² - 2BC × BD.
• In Fig. 6.60, AD is a median of a triangle ABC and AM ⊥ BC. Prove that : (i) AC² = AD² + BC.DM + (BC/2)² (ii) AB² = AD² - BC.DM + (BC/2)² (iii) AC² + AB² = 2AD² + 1/2BC²