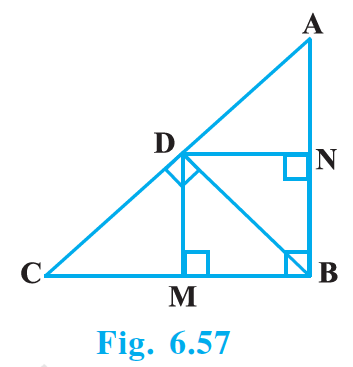
In Fig. 6.57, D is a point on hypotenuse AC of ΔABC, such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that:
(i) DM² = DN.MC   (ii) DN² = DM.AN

Solution:

From the given figure we see that, DMBN is a rectangle.

DM = BN and DN = BM ......... (i)

(i) In ΔDCM,

∠DCM + ∠DMC + ∠CDM = 180°

∠DCM + 90° + ∠CDM = 180°

∠DCM + ∠CDM = 90°........ (ii)

But ∠CDM + ∠BDM = 90°....... (iii) [Since BD ⊥ AC]

From (ii) and (iii)

∠DCM = ∠BDM................ (iv)

In ΔBDM,

∠DBM + ∠BDM = 90°................ (v) [Since, DM ⊥ BC]

From (iii) and (v)

∠CDM = ∠DBM.............(vi)

Now in ΔDCM and ΔDBM

ΔDCM ~ ΔBDM [From (iv) and (vi), AA criterion]

DM/BM = MC/DM [Corresponding sides are in same ratio]

DM² = BM.MC

DM² = DN.MC [from (i) DN = BM]

(ii) In ΔBDN,

∠BDN + ∠DBN = 90° [Since DN ⊥ AB]........ (vii)

But ∠ADN + ∠BDN = 90° [Since BD ⊥ AC]....... (viii)

From (vii) and (viii)

∠DBN = ∠ADN..........(ix)

In ΔADN,

∠DAN + ∠ADN = 90° [Since DN ⊥ AB]......... (x)

But ∠BDN + ∠ADN = 90° [Since BD ⊥ AC]......... (xi)

From (xi) and (x)

∠DAN = ∠BDN......... (xii)

Now, in ΔBDN and ΔDAN ,

ΔBDN ~ ΔDAN [From (ix) and (xii), AA criterion]

BN/DN = DN/AN [Basic proportionality theorem]

DN² = BN.AN

DN² = DM.AN [From (i) BN = DM ]

☛ Check: NCERT Solutions Class 10 Maths Chapter 6

---

Video Solution:

In Fig. 6.57, D is a point on hypotenuse AC of ΔABC, such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that: (i) DM² = DN.MC (ii) DN² = DM.AN

NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.6 Question 2

Summary:

In the above figure, D is a point on hypotenuse AC of ΔABC, such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Hence it is proved that  (i) DM² = DN.MC (ii) DN² = DM.AN

---

☛ Related Questions:

• In Fig. 6.58, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that: AC² = AB² + BC² + 2BC.BD.
• In Fig. 6.59, ABC is a triangle in which ∠ABC less than 90° and AD ⊥ BC. Prove that: AC² = AB² + BC² - 2BC × BD.
• In Fig. 6.60, AD is a median of a triangle ABC and AM ⊥ BC. Prove that : (i) AC² = AD² + BC.DM + (BC/2)² (ii) AB² = AD² - BC.DM + (BC/2)² (iii) AC² + AB² = 2AD² + 1/2BC²
• Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.