NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.2 Areas Related to Circles
NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2 Areas Related to Circles helps students explore the concept of sector and segment. A sector can be defined as the portion of the circular region enclosed by two radii and the corresponding arc while the part of the circular region enclosed between a chord and the corresponding arc is called a segment. In this exercise, kids are required to find the area of a segment or a sector through a variety of sums. There is a gradual increase in the level of difficulty allowing kids to experience a range of problems. NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.2 has a pool of 14 questions that range from easy to difficult. Some sums might directly ask a child to apply a formula while some might require a display of exceptional mathematical skills.
The complex questions in this exercise see a blend of concepts. For example, to find the area of a segment a child might have to apply congruence of triangles as well as the properties of circles. Another point to note is that a sector and segment can be divided into major and minor portions. Thus, it is important to be mindful of these concepts while attempting such problems. To learn more the scrollable PDF block of Class 10 Maths NCERT Solutions Chapter 12 Exercise 12.2 Areas Related to Circles is given below:
☛ Download NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.2
Exercise 12.2 Class 10 Chapter 12



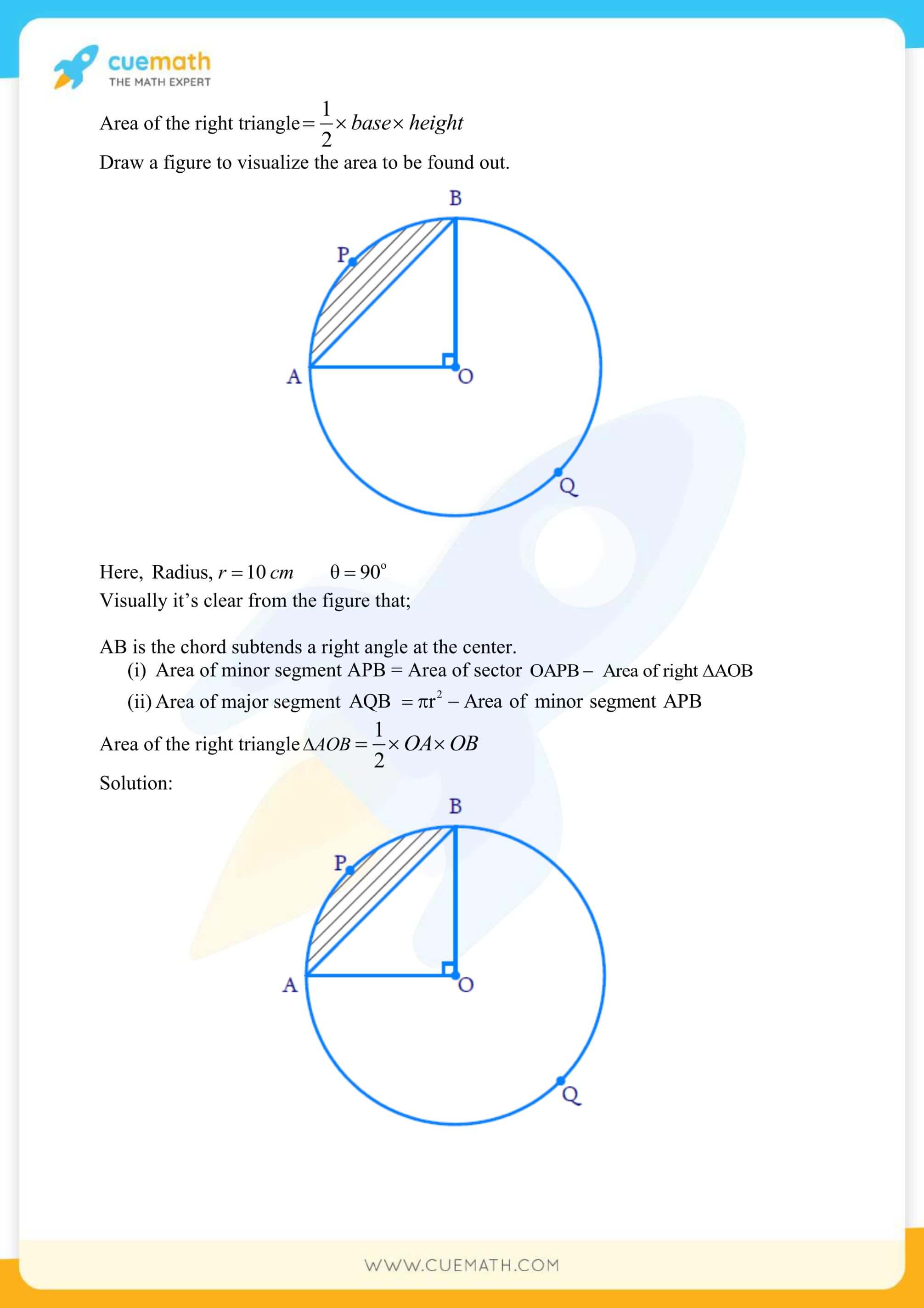

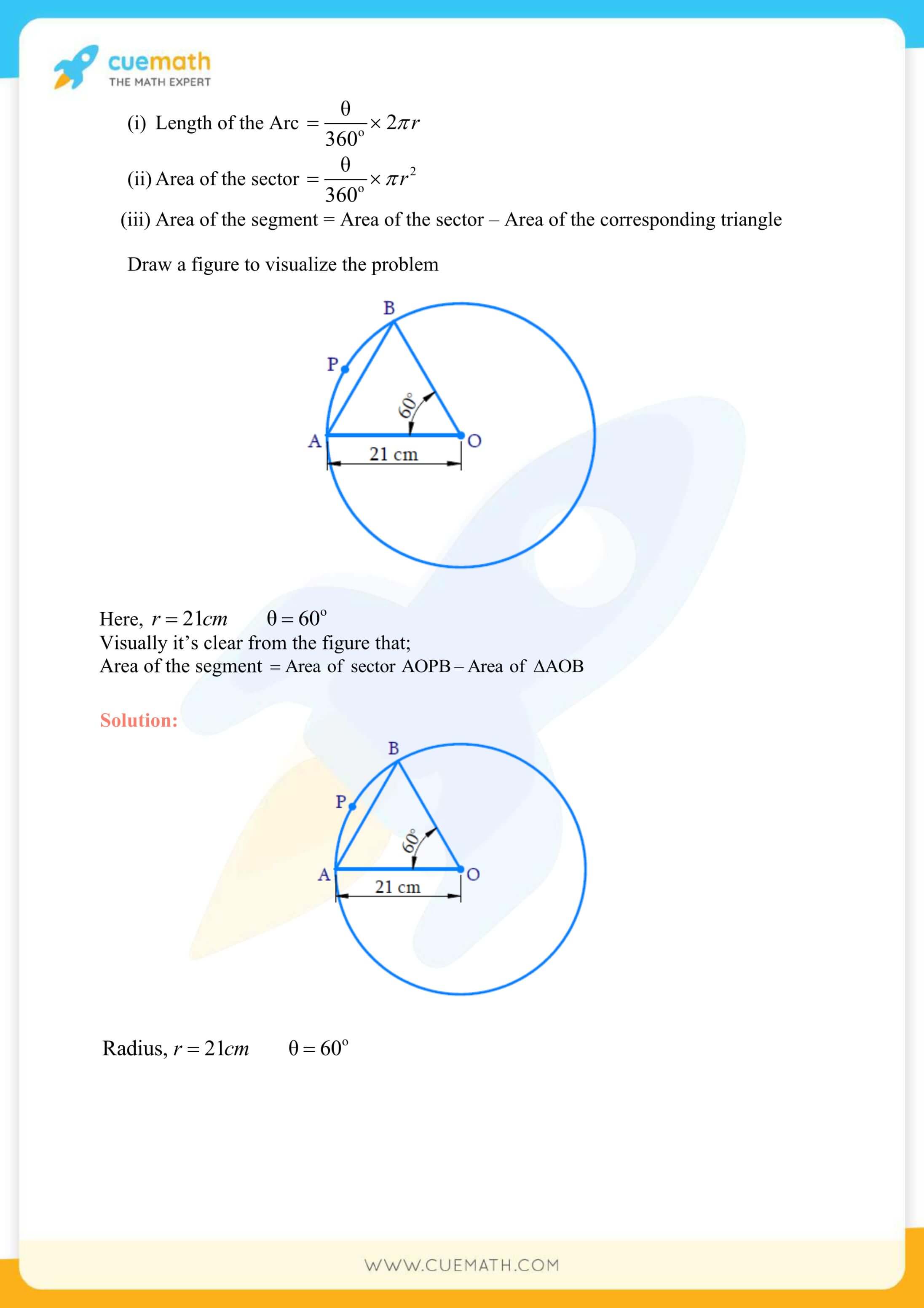


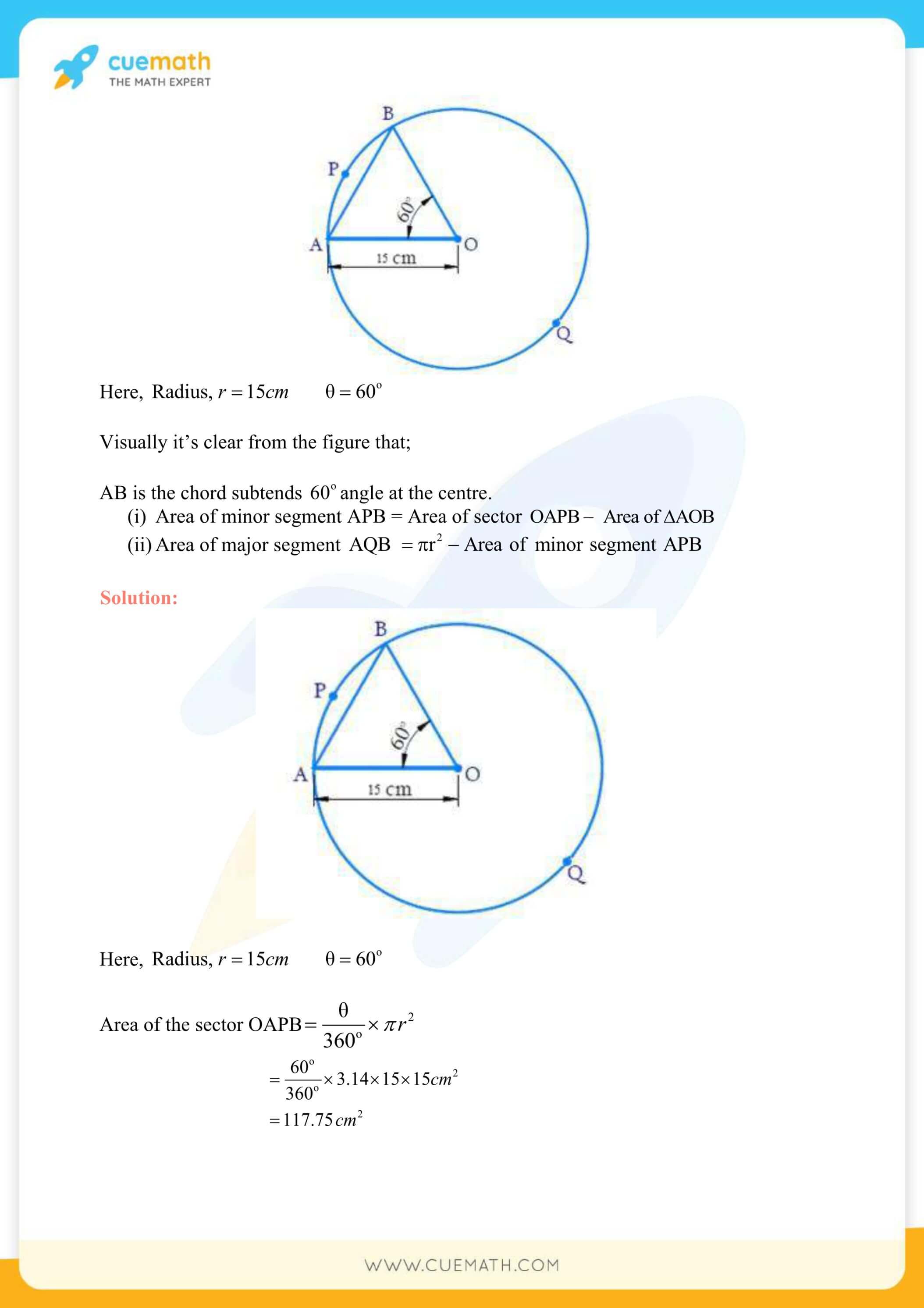
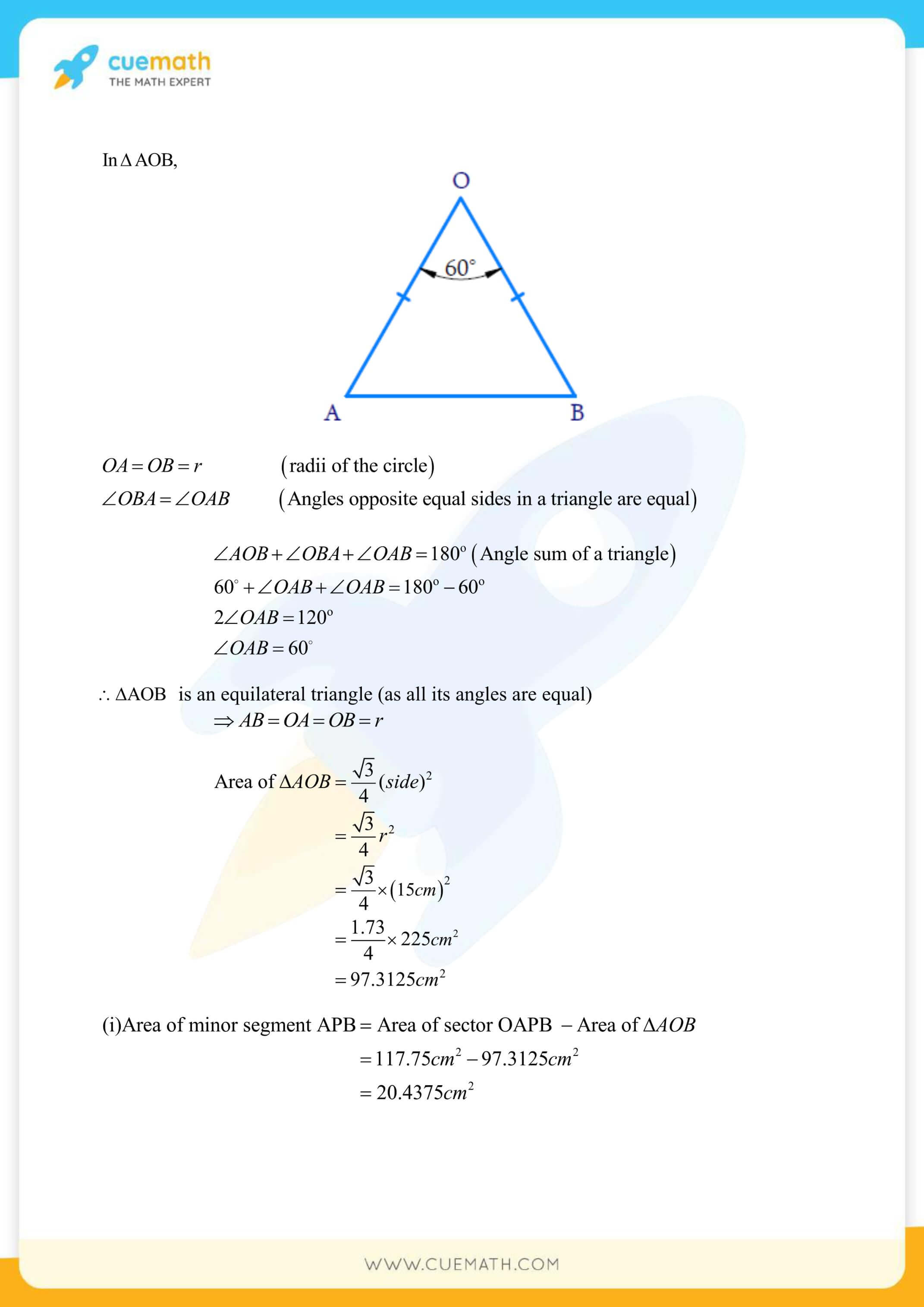















More Exercises in Class 10 Maths Chapter 12
NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.2 Formulas
NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.2 Areas Related to Circles have certain important formulas that are crucial for attempting these questions.
- Area of the sector of angle θ = (θ/360)×πr2. To get this formula we consider the entire circular section to be a sector measuring 360°. We then apply the unitary method and area of a circle, i.e., πr2 to derive the required formula. In other words, if the degree measure of the angle at the center is 360° then the area is πr2. Thus, when the degree measure of the angle is θ then the area will be given by the above-mentioned formula.
- Length of an arc of a sector of angle θ = (θ/360)×2π We use a similar procedure as above to find this formula. This means that we use the unitary method as well as the circumference of the circle given by 2πr to derive this formula.
- Area of major sector = πr 2 – Area of the minor sector. This is a simple application of subtracting a small part of an area from the complete figure to get the desired area.
- Area of major segment = πr 2 – Area of the minor segment.
Download Cuemath NCERT Solutions PDF for free and start learning!
NCERT Class 10 Maths Video Solutions Chapter 12 Exercise 12.2
| NCERT Videos for Class 10 Maths Chapter 12 Exercise 12.2 | |
|---|---|
| Question 1 | Question 8 |
| Question 2 | Question 9 |
| Question 3 | Question 10 |
| Question 4 | Question 11 |
| Question 5 | Question 12 |
| Question 6 | Question 13 |
| Question 7 | Question 14 |
visual curriculum