CBSE NCERT Class 9 Maths Chapter 4 Exercise 4.3 Solutions

Given: Linear equation 3y = ax + 7. We can find the value of 'a' by substituting the values of x and y in the given equation By substituting the value of x = 3 and y = 4 in the the equation 3y = ax + 7, we get

A day full of math games & activities. Find one near you.

NCERT Solutions Class 9 Maths Chapter 4 Exercise 4.3 Linear Equations in two Variables

NCERT solutions class 9 maths Chapter 4 exercise 4.3 linear equations in two variables comprise questions based on the geometrical representation of linear equations. These NCERT solutions are highly competent resources for gaining an in-depth understanding of graphs and plotting solutions of linear equations on a coordinate plane. NCERT solutions class 9 maths Chapter 4 exercise 4.3 has a total of 8 questions that adequately cover these concepts in detail.

NCERT Solutions are an excellent means to promote the understanding of core algebra concepts required for advanced math studies. To learn more about graphing linear equations, you can download the NCERT Solutions Class 9 Maths Chapter 4 exercise 4.3 in a scrollable PDF format as given below.

☛ Download NCERT Solutions Class 9 Maths Chapter 4 Exercise 4.3

Exercise 4.3 Class 9 Chapter 4

$NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 9$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 10$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 11$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 12$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 13$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 14$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 15$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 16$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 17$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 18$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 19$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 20$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 21$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 22$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 23$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 24$ $NCERT Solutions Class 9 Math Chapter 4 Exercise 4.3 25$

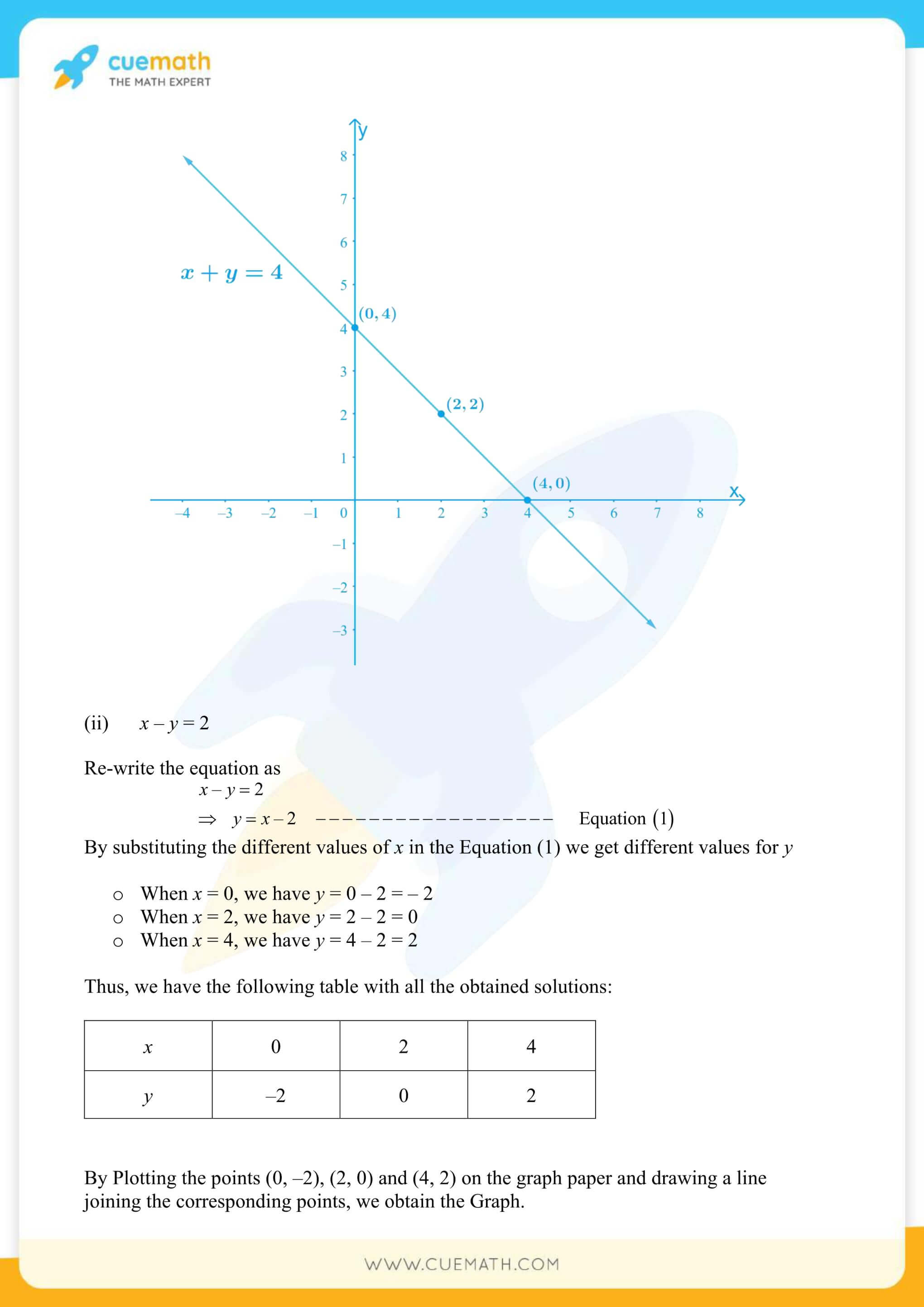
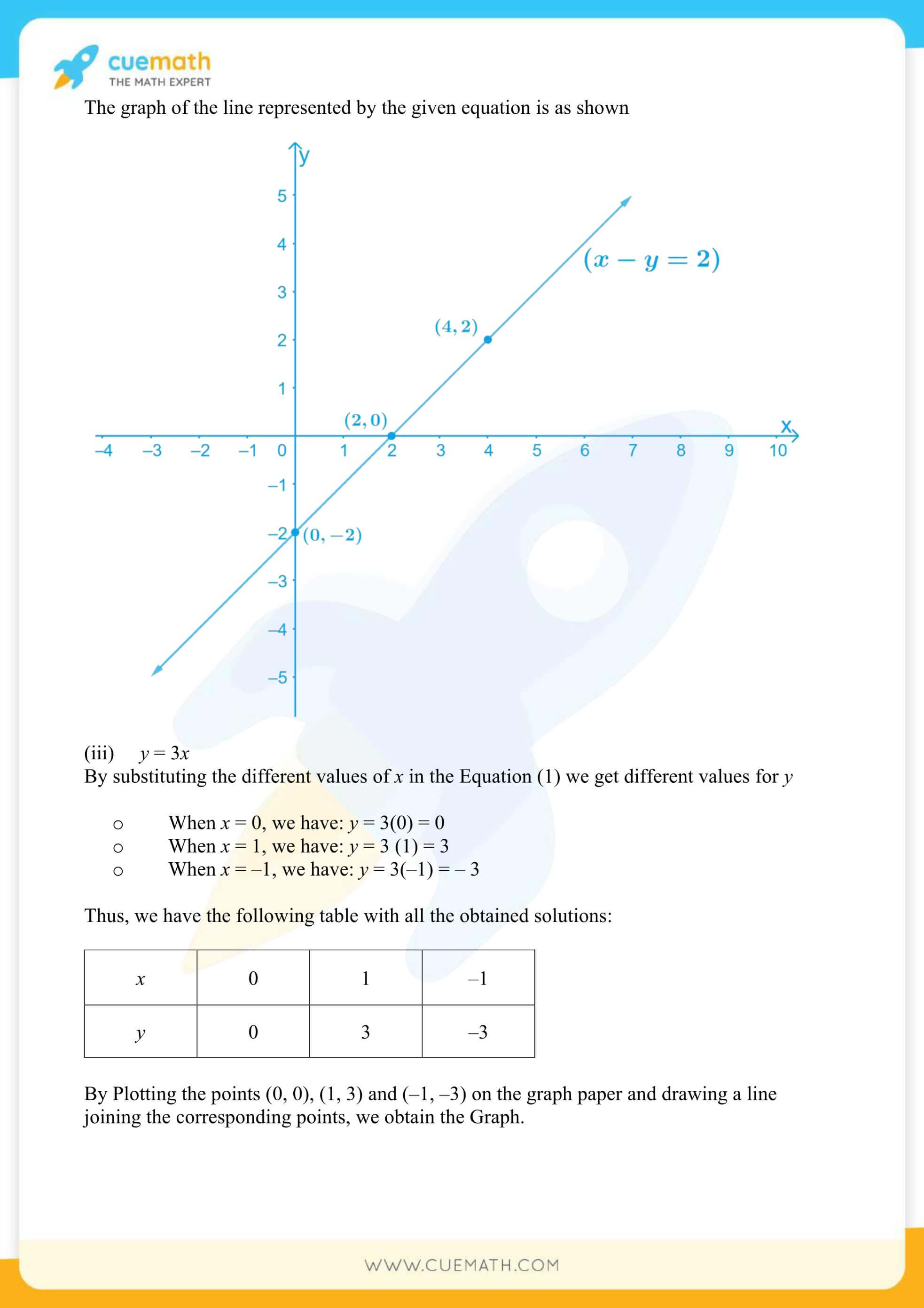
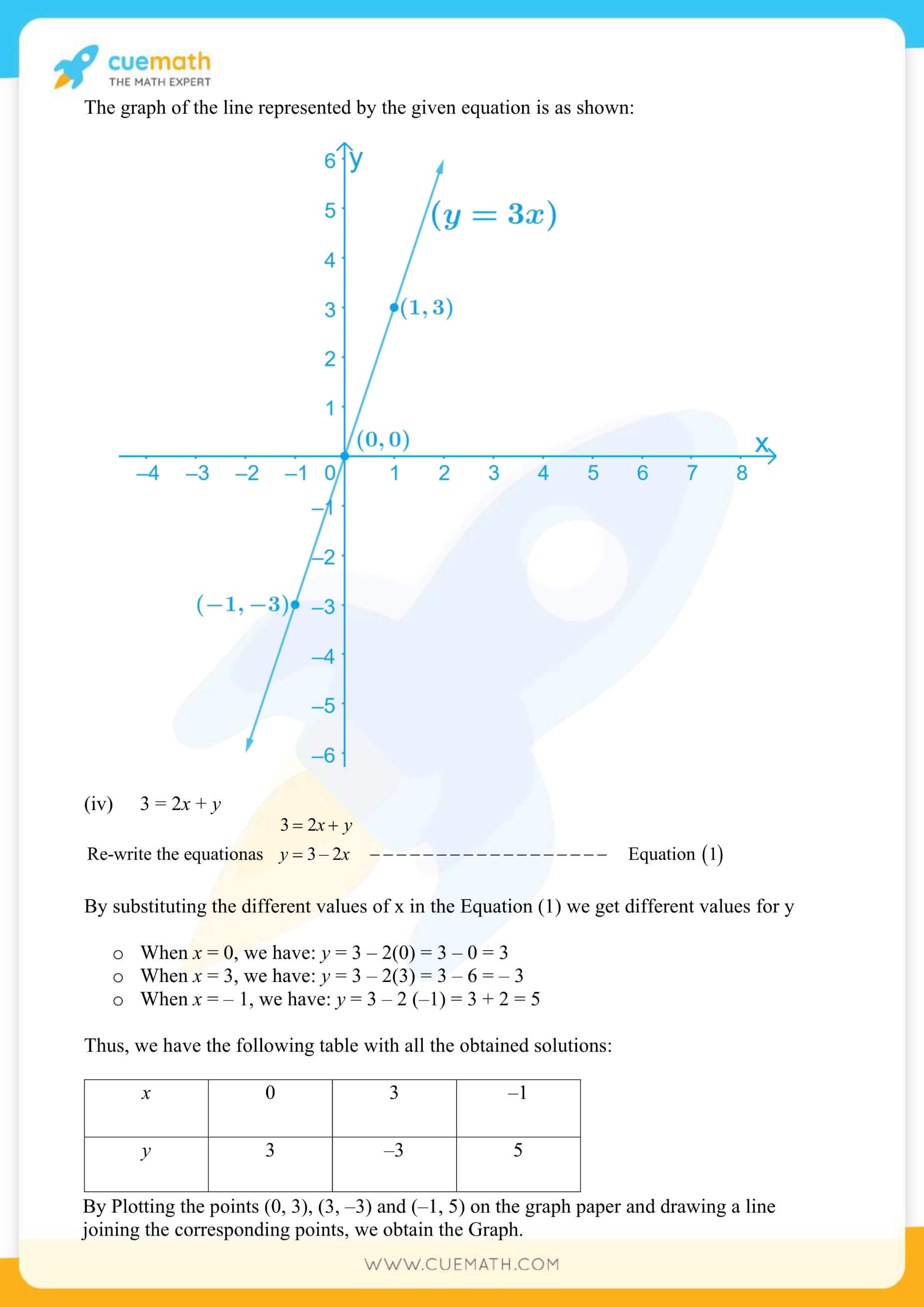
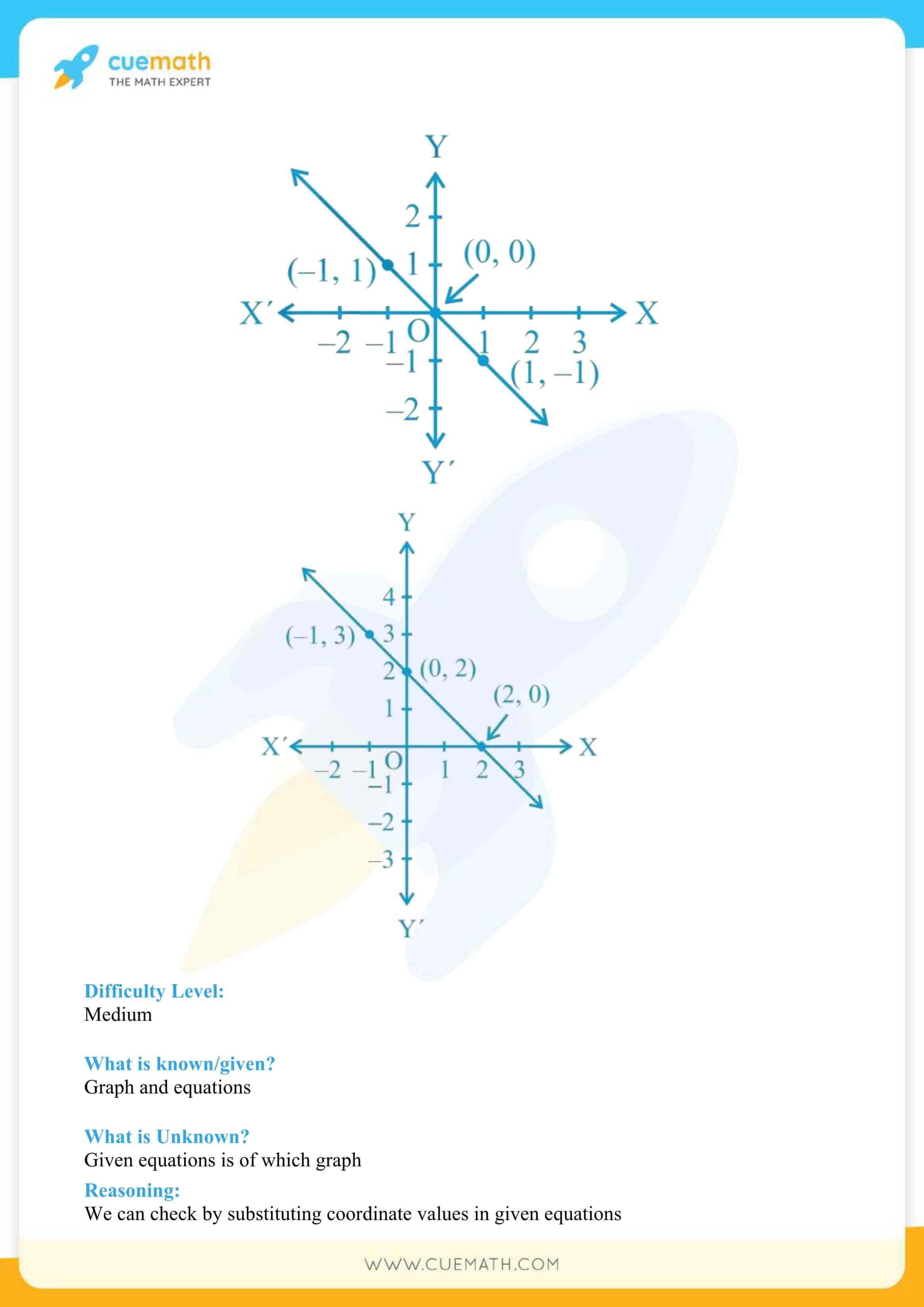
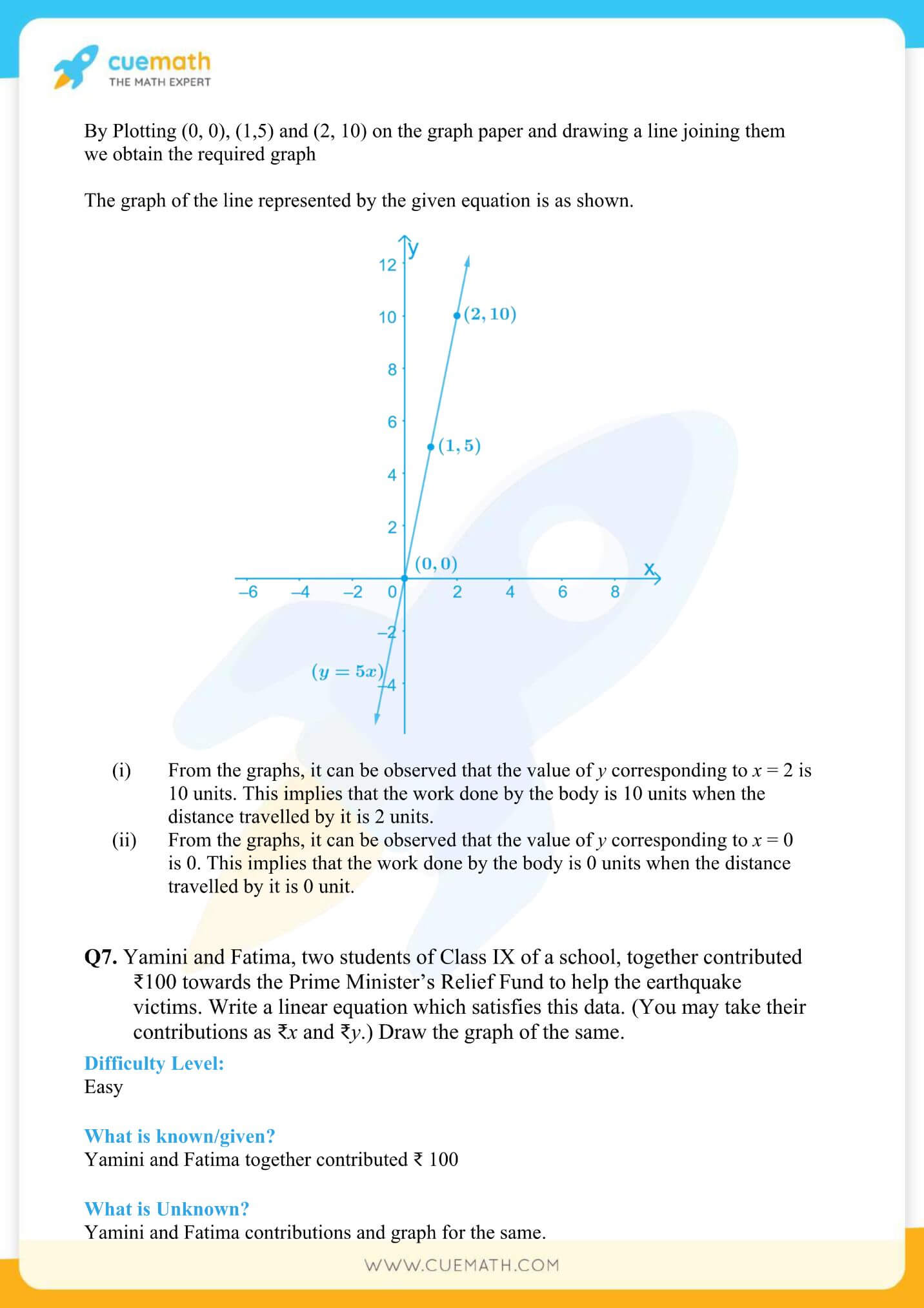
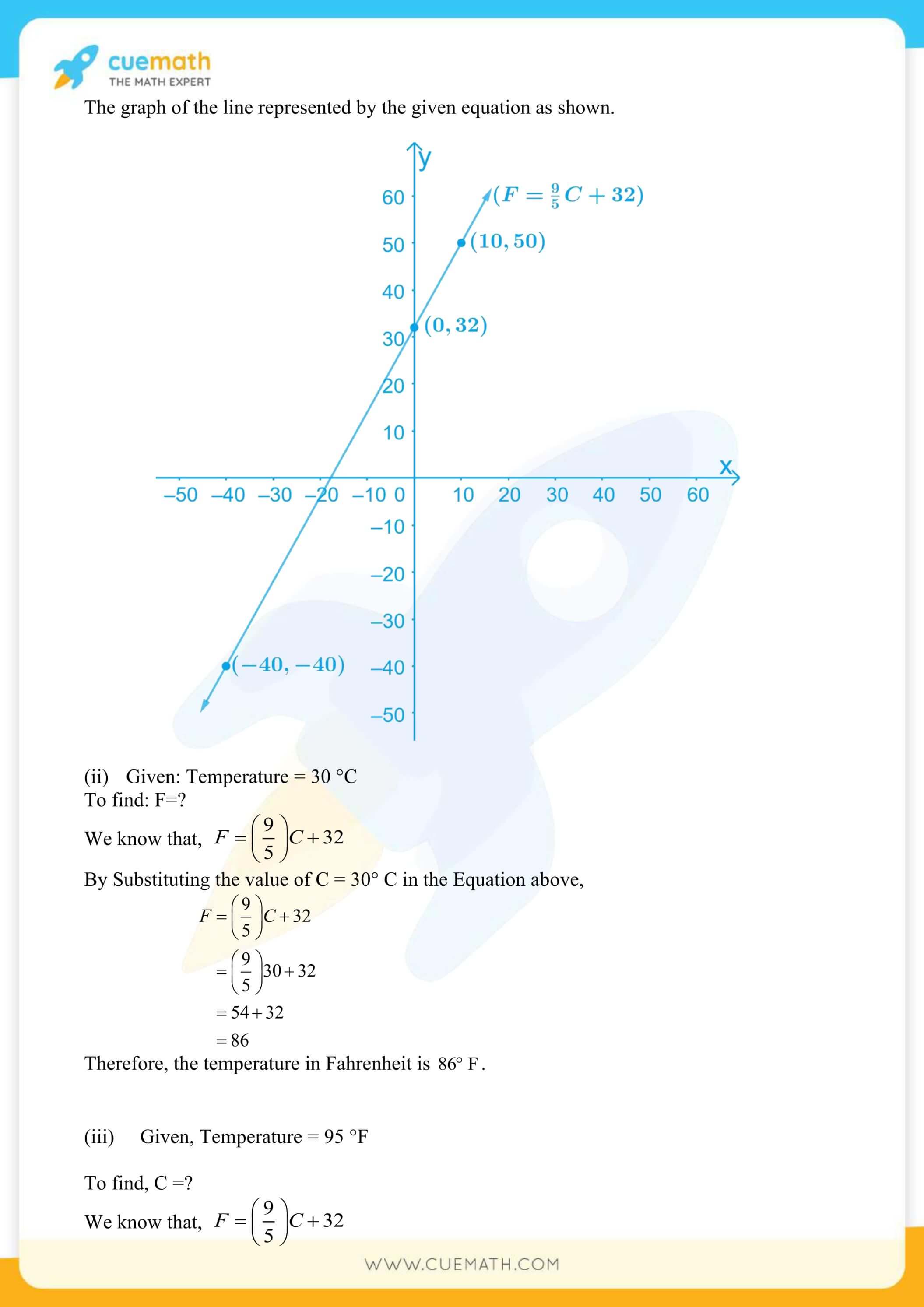
More Exercises in Class 9 Maths Chapter 4

NCERT Solutions Class 9 Maths Chapter 4 Exercise 4.3 Tips

Students will attain an in-depth understanding of the graph of linear equations in two variables through the practice of all the questions included in the NCERT solutions class 9 maths Chapter 4 exercise 4.3. By reading through the content provided in the NCERT Solutions Class 9 Maths Chapter 4 Exercise 4.3, students can grasp these concepts easily and apply them comfortably.

Making notes of the important key concepts and formulas included in the NCERT solutions class 9 maths chapter 4 exercise 4.3 will benefit the students to memorize them fast. Doing so will also help students to prepare for the exam through a quick revision. It is why students need to read and understand Class 9 Maths Chapter 4 Exercise 4.3.

Download Cuemath NCERT Solutions PDFs for free and start learning!

Class 9 Maths NCERT Solutions Video Chapter 4 Exercise 4.3

NCERT Video Solutions for Class 9 Maths Chapter 4 Exercise 4.3
Chapter 4 Exercise 4.3 Question 1	Chapter 4 Exercise 4.3 Question 5
Chapter 4 Exercise 4.3 Question 2	Chapter 4 Exercise 4.3 Question 6
Chapter 4 Exercise 4.3 Question 3	Chapter 4 Exercise 4.3 Question 7
Chapter 4 Exercise 4.3 Question 4	Chapter 4 Exercise 4.3 Question 8

Math worksheets and
visual curriculum