Present Value Formula

The present value formula refers to the application of the time value of money that discounts the future cash flow to arrive at its present-day value. The present value formula consists of the present value and future value related to compound interest. The present value or PV is the initial amount (the amount invested, the amount lent, the amount borrowed, etc). The future value or FV is the final amount. i.e., FV = PV + interest.  Let us understand the present value formula in detail in the following section.

What is the Present Value Formula?

Present value (PV) formula finds application in finance to calculate the present day value of an amount that is received at a future date. The present value formula (PV formula) is derived from the compound interest formula. The compound interest formula is,

FV = PV (1 + r / n)^nt

Dividing both sides by (1 + r / n)^nt,

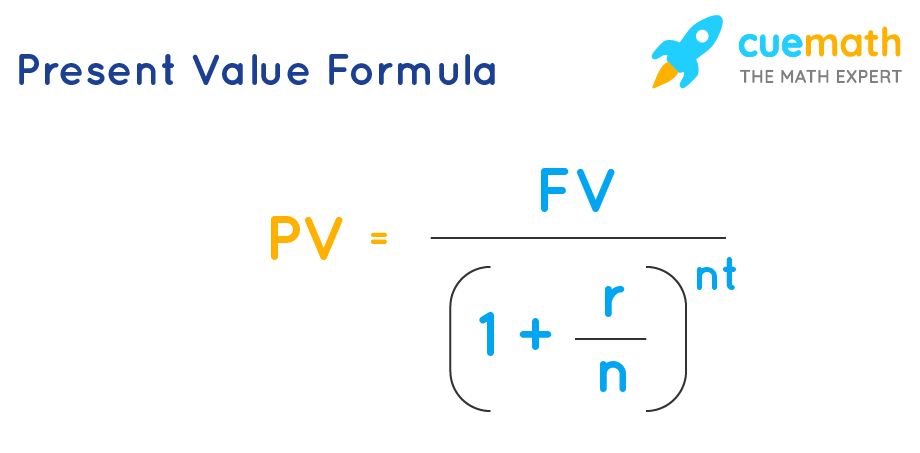
PV = FV / (1 + r / n)^nt

Thus, the present value formula is:

PV = FV / (1 + r / n)^nt

Where,

• PV = Present value
• FV = Future value
• r = Rate of interest (percentage ÷ 100)
• n = Number of times the amount is compounding
• t = Time in years

The value of n varies depending on the number of times the amount is compounding.

• n = 1, if the amount is compounded yearly.
• n = 2, if the amount is compounded half-yearly.
• n = 4, if the amount is compounded quart-yearly.
• n = 12, if the amount is compounded monthly.
• n = 52, if the amount is compounded weekly.
• n = 365, if the amount is compounded daily.

Examples Using Present Value Formula 

Example 1: Jonathan borrowed some amount from a bank at a rate of 7% per annum compounded annually. If he finished paying his loan by paying $6,500 at the end of 4 years, then what is the amount of loan that he had taken? Round your answer to the nearest thousands.

Solution:

The future value is, FV = $6500.

The time is t = 4 years.

n = 1 (as the amount is compounded annually).

The rate of interest is, r = 7% =0.07.

Substitute all these values in the the present value formula:

PV = FV / (1 + r / n)^nt

PV = 6500 / (1 + 0.07/1)¹⁽⁴⁾ = 6500 / (1.07)⁴ = 5,000 (The answer is rounded to the nearest thousands).

Therefore, the borrowed amount = $5,000

Example 2: Mia invested some amount in a bank where her amount gets compounded daily at 5% annual interest. What is the amount invested by Mia if the amount she got after 10 years is $1,650? Round your answer to the nearest thousands.

Solution:

The future value is, FV = $1650.

The time, t = 10 years.

n = 365 (as the amount is compounded daily).

The rate of interest is, r = 5% =0.05.

Substitute all these values in the present value formula:

PV = FV / (1 + r / n)^{n t} 

PV = 1650 / (1 + 0.05/365)^365(10) = 1000 (The answer is rounded to the nearest thousands).

Therefore, the invested amount = $1,000

Example 3: Josie borrowed some amount from a bank at a rate of 5% per annum compounded annually. If she finished paying her loan by paying $4,500 at the end of 4 years, then what is the amount of loan that she had taken? Round your answer to the nearest thousands.

Solution: 

The future value is, FV = $4500.

The time is t = 4 years.

n = 1 (as the amount is compounded annually).

The rate of interest is, r = 5% =0.05.

Substitute all these values in the the present value formula:

PV = FV / (1 + r / n)^nt

PV = 4500 / (1 + 0.05/1)¹⁽⁴⁾ = 4500 / (1.05)⁴ = 3,800 (The answer is rounded to the nearest thousands).

Therefore, the borrowed amount = $3,800