How to find the domain of a function on a graph?

The domain of a function is defined as the set of all possible input values.

Answer: A domain is the set of ‘all the values’ that go into a function. The domain of a function is all the possible values of the independent variable x, for which y is defined.

Let's understand the domain.

Explanation:

A domain is ‘all the values’ that go into a function. The domain of a function is all the possible values of the independent variable x, for which y is defined. The range of a function is all the possible output values of the function.

Finding Domain:

In a given ordered pair (x,y), the domain is defined as the set of all first elements of ordered pairs (x-coordinates). Thus, on a graph, the domain can be found by the set of values towards the direction of the x-axis.

Let's take an example to understand the calculation of domain.

Example: Find the domain of the function given below.

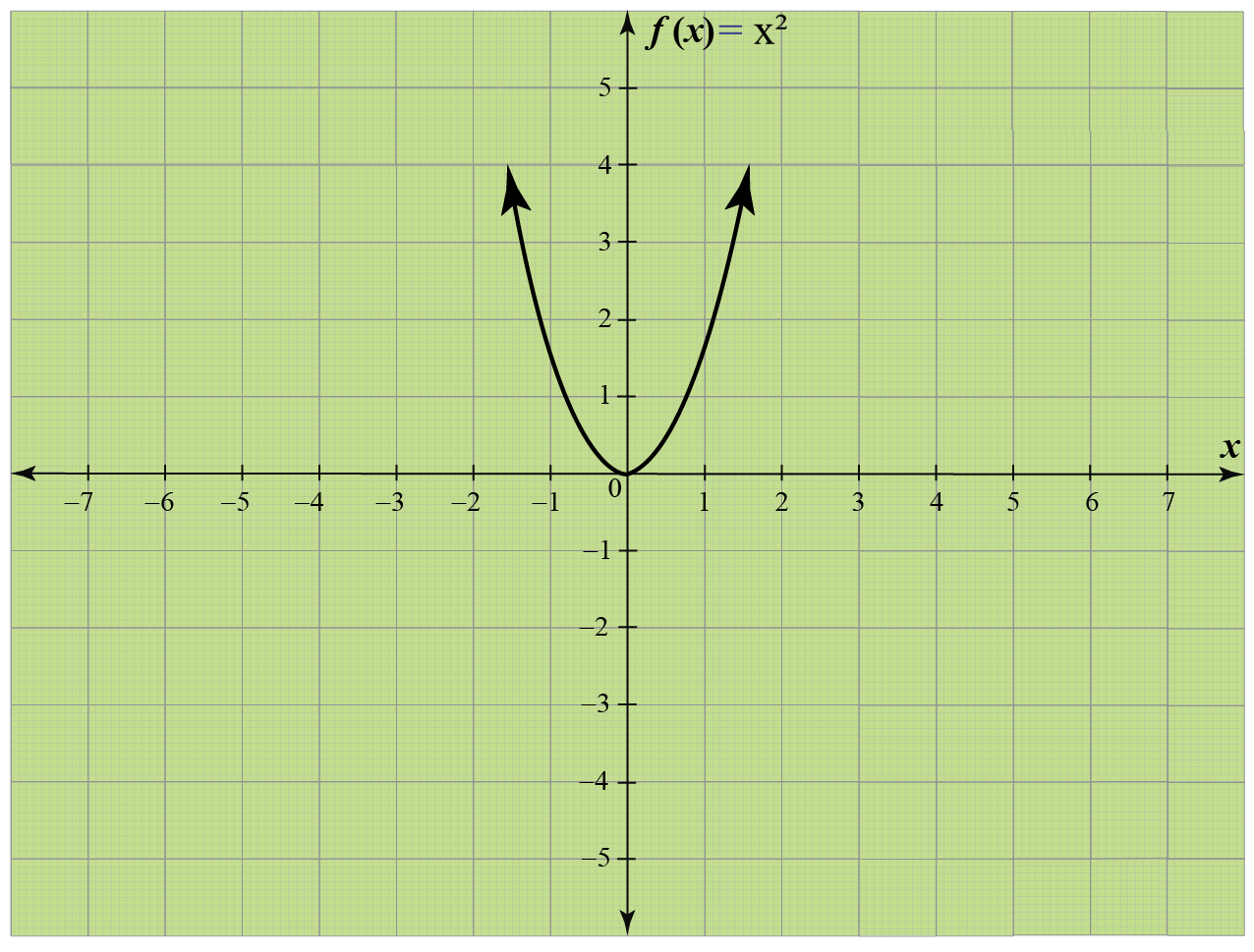
Solution: 

We observe from the graph that the horizontal extent of the graph is from (−∞,∞).

So, the domain is (−∞,∞).

Thus, for a quadratic function f(x) = x², the domain is all real numbers.

Hence, the domain of the given function graph is (−∞,∞).