Which triangle is similar to △ABC if sin(A) = 1/4, cos(A) = √15/4, and tan(A) = 1/√15?

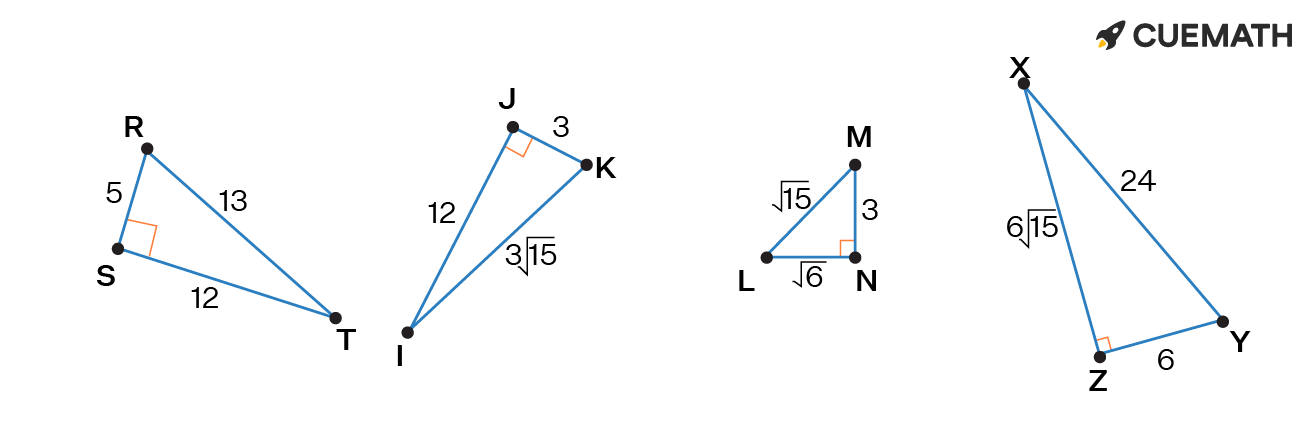
Solution:

Given, sin(A) = 1/4

cos(A) = √15/4

tan(A) = 1/√15

We have to find a triangle similar to triangle ABC.

We know, sin(x) = opposite/hypotenuse

cos(x) = adjacent/hypotenuse

tan(x) = opposite/adjacent

From the figures given in option,

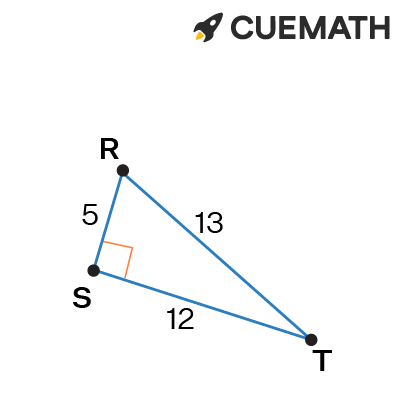
a) sin(R) = 12/13

cos(R) = 5/13

tan(R) = 12/5

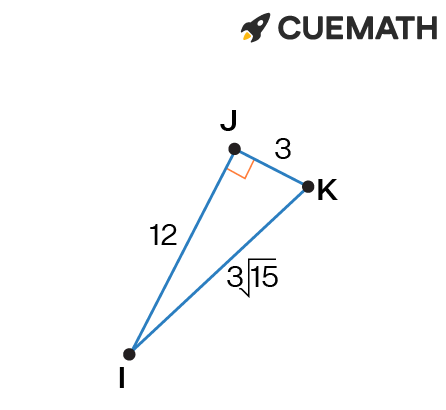
b) sin(K) = 12/3√15 = 4/√15

cos(K) = 3/3√15 = 1/√15

tan(K) = 12/3 = 4

c) sin(L) = 3/√15

cos(L) = √6/√15

tan(L) = 3/√6

d) sin(X) = 6/24 = 1/4

cos(X) = 6√15/24 = √15/4

tan(X) = 6/6√15 = 1/√15

Therefore, triangle XYZ is similar to triangle ABC.

---

Which triangle is similar to △ABC if sin(A) = 1/4, cos(A) = √15/4, and tan(A) = 1/√15?

Summary:

Triangle XYZ is similar to △ABC if sin(A) = 1/4, cos(A) = √15/4, and tan(A) = 1/√15.