Applications of Quadratics
Quadratic equations arise in a lot of practical scenarios. Here are a few examples:
Solved Example 1: The product of two consecutive even integers is equal to 24. Find these integers.
Solution: Let the two integers be \(x,\,\,x + 2\). We have:
\[\begin{align}&x\left( {x + 2} \right) = 24\\&\Rightarrow \,\,\,{x^2} + 2x - 24 = 0\\&\Rightarrow \,\,\,\left( {x + 6} \right)\left( {x - 4} \right) = 0\\&\Rightarrow \,\,\,x = - 6,\,\,x = 4\end{align}\]
Thus, two pairs of such integers exist:
\[\left( { - 6, - 4} \right), \left( {4,6} \right)\]
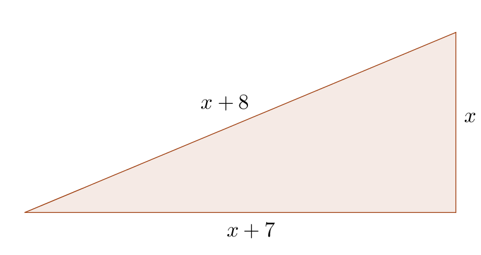
Solved Example 2: The sides of a right-angle triangle have the following lengths:
\[x,\,\,x + 7,\,\,x + 8\]
What is the area of the triangle?
Solution: The Pythagoras Theorem tells us that the sum of the squares of the smaller two sides of a right-angled triangle will be equal to the hypotenuse (longest side) squared.
In this case, we thus have:
\[\begin{align}&{x^2} + {\left( {x + 7} \right)^2} = {\left( {x + 8} \right)^2}\\&\Rightarrow \,\,\,{x^2} + {x^2} + 14x + 49 = {x^2} + 16x + 64\\&\Rightarrow \,\,\,{x^2} - 2x - 15 = 0\\&\Rightarrow \,\,\,\left( {x + 3} \right)\left( {x - 5} \right) = 0\\&\Rightarrow \,\,\,x = - 3,\,\,5\end{align}\]
We discard the first value since a side cannot have a negative length. Thus, \(x = 5\), and the three sides of the triangle are \(5,\,\,12,\,\,13\). The area is:
\[A = \frac{1}{2} \times 5 \times 12 = 30\,\,{\rm{sq}}{\rm{.}}\,\,{\rm{units}}\]
Solved Example 3: Two water taps can together fill a tank in \(9\frac{3}{8}\) hours. The tap with the larger opening takes 10 hours less than the tap with the smaller opening to fill the tank (separately). What is the time in which the larger tap can fill the tank?
Solution: Let V be the volume of the tank. Suppose that the smaller tap takes x hours to fill the tank (by itself). Then, the larger tap will take \(\left( {x - 10} \right)\) hours to fill the tank. The rate of flow from the two taps is \(\frac{V}{x}\) and \(\frac{V}{{x + 10}}\) units / hour. Thus, together the two taps have a total outflow of \(\frac{V}{x} + \frac{V}{{x + 10}}\) units / hour.
It is given that the two taps can together fill the tank in \(9\frac{3}{8}\) hours or \(\frac{{75}}{8}\) hours. In one hour, the two taps can therefore fill \(\frac{8}{{75}}\) of the total volume V.
Thus,
\[\begin{align}&\frac{V}{x} + \frac{V}{{x + 10}} = \frac{{8V}}{{75}}\\&\Rightarrow \,\,\,\frac{1}{x} + \frac{1}{{x + 10}} = \frac{8}{{75}}\end{align}\]
Rearranging, this can be modified to a quadratic equation (verify):
\[\begin{align}&4{x^2} - 115x + 375 = 0\\&\Rightarrow \,\,\,4{x^2} - 100x - 15x - 375 = 0\\&\Rightarrow \,\,\,4x\left( {x - 25} \right) - 15\left( {x - 25} \right) = 0\\&\Rightarrow \,\,\,\left( {4x - 15} \right)\left( {x - 25} \right) = 0\end{align}\]
Now that x cannot equal \(\frac{{15}}{4}\) since \(\left( {x - 10} \right)\) will then be negative. Thus, \(x = 25\). The smaller tap fills the tank in 25 hours, while the larger tap fills the tank in 15 hours.
Solved Example 4: A boat has a speed of 18 km/hr in still water. In a certain river, it takes 1 hour more to go 24 km upstream than to return to the same point. What is the speed at which water is flowing in the river?
Solution: Let the speed of the water flow be v km/hr. While going upstream, the speed of the boat (relative to the ground) will be \(\left( {18 - v} \right)\) km/hr, whereas, while going downstream, it will be \(\left( {18 + v} \right)\) km/hr.
The time taken in traveling 24 km upstream is \(\frac{{24}}{{18 - v}}\) hours. The time taken in traveling 24 km downstream is \(\frac{{24}}{{18 + v}}\) hours. The difference of these two times is 1 hour. Thus,
\[\frac{{24}}{{18 - v}} - \frac{{24}}{{18 + v}} = 1\]
Upon rearrangement, this can be written as the following quadratic equation (verify):
\[\begin{align}&{v^2} + 48v - 324 = 0\\&\Rightarrow \,\,\,{v^2} + 54v - 6v - 324 = 0\\&\Rightarrow \,\,\,v\left( {v + 54} \right) - 6\left( {v + 54} \right) = 0\\&\Rightarrow \,\,\,\left( {v - 6} \right)\left( {v + 54} \right) = 0\end{align}\]
Clearly, v equals 6 km/hr.
Solved Example 5: A narrow-gauge train takes 2 hours less for a journey of 300 km if its speed is increased by 5 km/hour from its normal speed. Find its normal speed.
Solution: We assume the normal speed to be x km/hour. At this speed, it will take \(\frac{{300}}{x}\) hours for the train to cover 300 km. At 5 km/hour faster, it will take \(\frac{{300}}{{x + 5}}\) hours for the train to cover the same distance.
The difference between these two times is 2 hours:
\[\begin{align}&\frac{{300}}{x} - \frac{{300}}{{x + 5}} = 2\\&\Rightarrow \,\,\,{x^2} + 5x - 750 = 0\\&\Rightarrow \,\,\,{x^2} + 30x - 25x - 750 = 0\\&\Rightarrow \,\,\,\left( {x - 25} \right)\left( {x + 30} \right) = 0\end{align}\]
Thus, \(x = 25\), that is, the normal speed of the train is 25 km/hour.
Solved Example 6: A certain piece of hand-crafted furniture can be completed by a craftsman P in 6 days less than the time taken by craftsman Q. If both work together, they can complete it in 4 days. In how many days can Q complete the task alone?
Solution: Suppose that it takes x days for Q to complete the piece alone. P will do the same job in \(\left( {x - 6} \right)\) days. In one day, P will do \(\frac{1}{{x - 6}}\) of the job and Q will do \(\frac{1}{x}\) of the job. Working together, they will do \(\frac{1}{x} + \frac{1}{{x - 6}}\) of the job.
It is also given that if both work together, they complete the piece in 4 days, that is, in one day, they can complete one-fourth of the piece, working together. Thus,
\[\begin{align}&\frac{1}{x} + \frac{1}{{x - 6}} = \frac{1}{4}\\&\Rightarrow \,\,\,{x^2} - 14x + 24 = 0\\&\Rightarrow \,\,\,\left( {x - 12} \right)\left( {x - 2} \right) = 0\end{align}\]
Since x cannot be 2 (why?), we have \(x = 12\). Thus, Q can complete the piece in 12 days, working alone.