Overview of Graphical Approach in Linear Equations

Let us summarize the three cases possible with respect to a pair of linear equations.

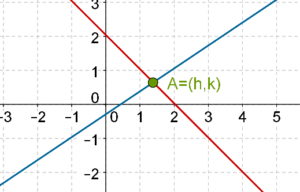
Case-1: There is a unique solution

In this case, the two lines will intersect each other at a unique point. The coordinates of that point will be the solution to the pair of linear equations:

Case-2: There is no solution

In this case, the two lines will be parallel to each other, so that there is no common point (of intersection):

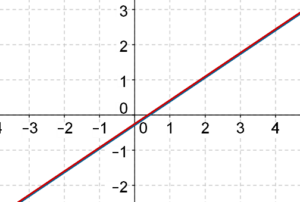
Case-3: There are infinitely many solutions

In this case, the two lines happen to coincide. This occurs because the two linear equations are essentially the same, if you remove an appropriate common factor from one of the two equations. In the following figure, we have drawn two lines which coincide, so there appears to be only one line: