Second Order Differential Equation
Second order differential equation is a specific type of differential equation that consists of a derivative of a function of order 2 and no other higher-order derivative of the function appears in the equation. It includes terms like y'', d2y/dx2, y''(x), etc. which indicates the second order derivative of the function. Generally, we write a second order differential equation as y'' + p(x)y' + q(x)y = f(x), where p(x), q(x), and f(x) are functions of x. We can solve this differential equation using the auxiliary equation and different methods such as the method of undetermined coefficients and variation of parameters.
The differential equation y'' + p(x)y' + q(x)y = 0 is called a second order differential equation with constant coefficients if the functions p(x) and q(x) are constants and it is called a second-order differential equation with variable coefficients if p(x) and q(x) are not constants. In this article, we will understand such differential equations in detail and their different types. We will also learn different methods to solve second order differential equations with constant coefficients using the various methods with the help of solved examples and finding the auxiliary equation.
| 1. | What is a Second Order Differential Equation? |
| 2. | Second Order Differential Equation Definition |
| 3. | Solving Second Order Differential Equation |
| 4. | FAQs on Second Order Differential Equation |
What is a Second Order Differential Equation?
A differential equation is an equation that consists of a function and its derivative. A differential equation that consists of a function and its second-order derivative is called a second order differential equation. Mathematically, it is written as y'' + p(x)y' + q(x)y = f(x), which is a non-homogeneous second order differential equation if f(x) is not equal to the zero function and p(x), q(x) are functions of x. It can also be written as F(x, y, y', y'') = 0. Further, let us explore the definitions of the different types of the second order differential equation.
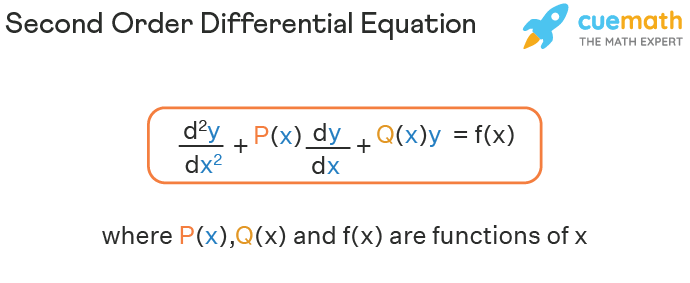
Second Order Differential Equation Definition
A second order differential equation is defined as a differential equation that includes a function and its second-order derivative and no other higher-order derivative of the function can appear in the equation. It can be of different types depending upon the power of the derivative and the functions involved. These differential equations can be solved using the auxiliary equation. Let us go through some special types of second order differential equations given below:
Linear Second Order Differential Equation
A linear second order differential equation is written as y'' + p(x)y' + q(x)y = f(x), where the power of the second derivative y'' is equal to one which makes the equation linear. Some of its examples are y'' + 6x = 5, y'' + xy' + y = 0, etc.
Homogeneous Second Order Differential Equation
A second order differential equation y'' + p(x)y' + q(x)y = f(x) is said to be a second order homogeneous differential equation if f(x) is a zero function and hence mathematically it of the form, y'' + p(x)y' + q(x)y = 0. Some of its examples are y'' + y' - 6y = 0, y'' - 9y' + 20y = 0, etc.
Non-homogeneous Second Order Differential Equation
A differential equation of the form y'' + p(x)y' + q(x)y = f(x) is said to be a non-homogeneous second order differential equation if f(x) is not a zero function. Some of its examples are y'' + y' - 6y = x, y'' - 9y' + 20y = sin x, etc.
Second Order Differential Equation with Constant Coefficients
The differential equation y'' + p(x)y' + q(x)y = f(x) is called a second order differential equation with constant coefficients if the functions p(x) and q(x) are constants. Some of its examples are y'' + y' - 6y = x, y'' - 9y' + 20y = sin x, etc.
Second Order Differential Equation with Variable Coefficients
The differential equation y'' + p(x)y' + q(x)y = f(x) is called a second order differential equation with variable coefficients if the functions p(x) and q(x) are not constant functions and are functions of x. Some of its examples are y'' + xy' - y sinx = x, y'' - 9x2y' + 2exy = 0, etc.
Solving Second Order Differential Equation
Now that we have understood the meaning of second order differential equation and their different forms, we shall proceed towards learning how to solve them. Here, we will focus on learning to solve 2nd differential equations with constant coefficients using the method of undetermined coefficients. First, let us understand how to solve the second order homogeneous differential equations.
Solving Homogeneous Second Order Differential Equation
A homogeneous second order differential equation with constant coefficients is of the form y'' + py' + qy = 0, where p, q are constants. To solve this, we assume a general solution y = erx of the given differential equation, where r is any constant, and follow the given steps:
- Step 1: Differentiate the assumed solution y = erx, and find y' = rerx, y'' = r2erx, where r is an arbitrary constant.
- Step 2: Substitute the derivatives in the given differential equation y'' + py' + qy = 0. We have r2erx + prerx + qerx = 0 ⇒ erx(r2 + rp + q) = 0 ⇒ r2 + rp + q = 0, which is called the auxiliary equation or characteristic equation.
- Step 3: Solve the auxiliary equation r2 + rp + q = 0 and find its roots r1 and r2.
- If r1 and r2 are real and distinct roots, then the general solution is y = Aer1x + Ber2x
- If r1 = r2 = r, then the general solution is y = Aerx + Bxerx
- If r1 = a + bi and r2 = a - bi are complex roots, then the general solution is y = eax(A sin bx + B cos bx)
Let us consider a few examples of each type to understand how to determine the solution of the homogeneous second order differential equation.
Example 1: Solve the 2nd order differential equation y'' - 6y' + 5y = 0
Solution: Assume y = erx and find its first and second derivative: y' = rerx, y'' = r2erx
Next, substitute the values of y, y', and y'' in y'' - 6y' + 5y = 0. We have,
r2erx - 6rerx + 5erx = 0
⇒ erx(r2 - 6r + 5) = 0
⇒ r2 - 6r + 5 = 0 → Characteristic Equation
⇒ (r - 5) (r - 1) = 0
⇒ r = 1, 5
Since the roots of the characteristic equation are distinct and real, therefore the general solution of the given differential equation is y = Aex + Be5x
Example 2: Solve the second order differential equation y'' - 8y' + 16y = 0
Solution: Assume y = erx and find its first and second derivative: y' = rerx, y'' = r2erx
Next, substitute the values of y, y', and y'' in y'' - 8y' + 16y = 0. We have,
r2erx - 8rerx + 16erx = 0
⇒ erx(r2 - 8r + 16) = 0
⇒ r2 - 8r + 16 = 0 → Auxiliary Equation
⇒ (r - 4) (r - 4) = 0
⇒ r = 4, 4
Since the roots of the characteristic equation are identical and real, therefore the general solution of the given differential equation is y = Ae4x + Bxe4x
Example 3: Solve the second order differential equation 9y'' + 12y' + 29y = 0
Solution: Assume y = erx and find its first and second derivative: y' = rerx, y'' = r2erx
Next, substitute the values of y, y', and y'' in 9y'' + 12y' + 29y = 0. We have,
9r2erx + 12rerx + 29erx = 0
⇒ erx(9r2 + 12r + 29) = 0
⇒ 9r2 + 12r + 29 = 0 → Characteristic Equation
⇒ r = [-12 ± √(122 - 4 × 9 × 29)]/(2 × 9)
⇒ r = (-2/3) ± (5/3)i
Since the roots of the characteristic equation are complex conjugates, therefore the general solution of the given second order differential equation is y = e(-2/3)x[A sin (5/3)x + B cos (5/3)x].
Solving Non-Homogeneous Second Order Differential Equation
To find the solution of Non-Homogeneous Second Order Differential Equation y'' + py' + qy = f(x), the general solution is of the form y = yc + yp, where yc is the complementary solution of the homogeneous second order differential equation y'' + py' + qy = 0 and yp is the particular solution of the non-homogeneous differential equation y'' + py' + qy = f(x). Since yc is the solution of the homogeneous differential equation, we can determine its value using the methods that we discussed in the previous section. Now, to find the particular solution yp, we can guess the solution depending upon the value of f(x). The table given below shows the possible particular solution yp corresponding to each f(x).
| f(x) | yp |
|---|---|
| beax | Aeax |
| axn + (lower order powers of x) | Cnxn + Cn-1xn-1 + ... + C0 |
| P cos ax or Q sin ax | A cos ax + B sin ax |
In case, f(x) is of a form other than the ones given in the table above, then we can use the method of variation of parameters to solve the non-homogeneous second order differential equation. Also, if f(x) is a sum combination of the functions given in the table, then we can determine the particular solution for each function separately and then take their sum to find the final particular solution of the given equation. Let us now consider a few examples of second order differential equations and solve them using the method of undetermined coefficients:
Example 1: Find the complete solution of the second order differential equation y'' - 6y' + 5y = e-3x.
Solution: To find the complete solution, first we will find the general solution of the homogeneous differential equation y'' - 6y' + 5y = 0.
We have solved this equation in the previous section in the solved examples (Example 1) and hence the complementary solution is yc = Aex + Be5x
Next, we will find the particular solution yp. Since f(x) = e-3x is of the form beax, let us assume yp = Ae-3x. Now differentiating yp, we have
yp' = -3Ae-3x and yp'' = 9Ae-3x . Substituting these values in the given second order differential equation, we have
yp'' - 6yp' + 5yp = e-3x
⇒ 9Ae-3x - 6(-3Ae-3x) + 5Ae-3x = e-3x
⇒Ae-3x (9 + 18 + 5) = e-3x
⇒ 32 A e-3x = e-3x
⇒ A = 1/32
Hence, the particular solution yp = (1/32) e-3x
Answer: Therefore, the complete solution of the given non-homogeneous 2nd order differential equation y'' - 6y' + 5y = e-3x is y = Aex + Be5x + (1/32) e-3x
Example 2: Solve the second order differential equation y'' - 6y' + 5y = cos 2x + e-3x
Solution: As we have solved the homogeneous differential equation y'' - 6y' + 5y = 0 in the previous section (Example 1), we have the complementary solution yc = Aex + Be5x
Next, we will find the particular solution of the given differential equation individually for cos 2x and e-3x, that is, determine the particular solution of y'' - 6y' + 5y = cos 2x and y'' - 6y' + 5y = e-3x separately. From example 1 above, we have the particular solution of the differential equation y'' - 6y' + 5y = e-3x corresponding to e-3x as (1/32) e-3x. Now, we will find the particular solution of the equation y'' - 6y' + 5y = cos 2x using the table. Assume the particular solution of the form Yp = A cos 2x + B sin 2x. Differentiating this, we have Yp' = -2A sin 2x + 2B cos 2x and Yp'' = -4A cos 2x - 4B sin 2x. Substituting these values in the differential equation y'' - 6y' + 5y = cos 2x, we have
-4A cos 2x - 4B sin 2x - 6(-2A sin 2x + 2B cos 2x) + 5(A cos 2x + B sin 2x) = cos 2x
⇒ -4A cos 2x - 4B sin 2x + 12A sin 2x - 12B cos 2x + 5A cos 2x + 5B sin 2x = cos 2x
⇒ (A - 12B) cos 2x + (B + 12A) sin 2x = cos 2x
⇒ A - 12B = 1 and B + 12A = 0
⇒ A = 1/145 and B = -12/145
⇒ Yp = (1/145) cos 2x - (12/145) sin 2x
Now, taking the sum of both particular solutions, the final particular solution of the given second order differential equation y'' - 6y' + 5y = cos 2x + e-3x is yp = (1/32) e-3x + (1/145) cos 2x - (12/145) sin 2x.
Answer: Therefore, the complete solution of the differential equation y'' - 6y' + 5y = cos 2x + e-3x is y = yc + yp = Aex + Be5x + (1/32) e-3x + (1/145) cos 2x - (12/145) sin 2x
Important Notes on Second Order Differential Equation
- If y1 and y2 are two linearly independent solutions of the homogeneous second order differential equation y'' + py' + qy = 0, then the particular solution of the corresponding second order non-homogeneous differential equation y'' + py' + qy = f(x) can be determined using the formula yp = -y1 ∫[y2 f(x)/W(y1, y2)] dx + y2 ∫[y1 f(x)/W(y1, y2)] dx, where W(y1, y2) = y1y2' - y2y1' is called the Wronskian. This method of finding the solution is called the method of variation of parameters.
- The method to find the solution of second-order differential equations with variable coefficients is complex and is based on guessing the solution.
☛ Related Topics:
Second Order Differential Equation Examples
-
Example 1: Solve the second order differential equation y'' - 9y' + 20y = 0
Solution: Since the given differential equation is homogeneous, we will assume the solution of the form y = erx
Find the first and second derivative of y = erx: y' = rerx, y'' = r2erx
Next, substitute the values of y, y', and y'' in y'' - 9y' + 20y = 0. We have,
r2erx - 9rerx + 20erx = 0
⇒ erx(r2 - 9r + 20) = 0
⇒ r2 - 9r + 20 = 0 → Auxiliary Equation
⇒ (r - 5) (r - 4) = 0
⇒ r = 4, 5
Since the roots of the characteristic equation are distinct and real, therefore the general solution of second order differential equation y'' - 9y' + 20y = 0 is y = Ae4x + Be5x
Answer: The solution y'' - 9y' + 20y = 0 is y = Ae4x + Be5x
-
Example 2: Find the complete solution of the second order differential equation y'' - y = 2x2 - x - 3
Solution: The given differential equation is a non-homogeneous second order differential equation, hence we need to find its complementary solution and particular solution separately.
First, we will find the solution yc of the homogeneous equation y'' - y = 0. For this, assume y = erx and find its first and second derivative: y' = rerx, y'' = r2erx
Next, substitute the values of y, y', and y'' in y'' - y = 0. We have,
r2erx - erx = 0
⇒ erx(r2 - 1) = 0
⇒ r2 - 1 = 0 → Auxiliary Equation
⇒ (r - 1) (r + 1) = 0
⇒ r = -1, 1
Since the roots of the characteristic equation are distinct and real, therefore the complementary solution is yc = Ae-x + Bex
Next, we will find the particular solution yp. For this, using the table, assume yp = Ax2 + Bx + C. Now find the derivatives of yp.
yp' = 2Ax + B and yp'' = 2A . Substituting these values in the given differential equation, we have
yp'' - yp = 2x2 - x - 3
⇒ 2A - (Ax2 + Bx + C) = 2x2 - x - 3
⇒ 2A - Ax2 - Bx - C = 2x2 - x - 3
⇒ -Ax2 - Bx + 2A - C = 2x2 - x - 3
⇒ -A = 2, -B = -1, 2A - C = -3
⇒ A = -2, B = 1, C = -1
⇒ yp = -2x2 + x - 1
The complete solution is y = yc + yp = Ae-x + Bex - 2x2 + x - 1
Answer: The complete solution of y'' - y = 2x2 - x - 3 is y = Ae-x + Bex - 2x2 + x - 1.

FAQs on Second Order Differential Equation
What is Second Order Differential Equation in Calculus?
A second order differential equation is defined as a differential equation that includes a function and its second-order derivative and no other higher-order derivative of the function can appear in the equation. It includes terms like y'', d2y/dx2, y''(x), etc. It can be of different types such as second-order linear differential equation, 2nd order homogeneous and non-homogeneous differential equation, and second-order differential equation with variable and constant coefficients.
How to Solve Second Order Differential Equation?
Second order differential equations can be solved using different methods such as the method of undetermined coefficients and the method of variation of parameters. The solution of a non-homogeneous second order differential is the sum of the complementary and particular solution and is given as y = yc + yp.
What is Second Order Differential Equation with Constant Coefficients?
A Second Order Differential Equation with Constant Coefficients is a differential equation of the form y'' + py' + qy = f(x), where p, q are constant coefficients.
What are Homogeneous and Non-Homogeneous Second Order Differential Equations?
A second order differential equation of the form y'' + py' + qy = f(x) is homogeneous if f(x) is a zero function and non-homogeneous if f(x) is not a zero function and is some non-zero function of x.
Why Does a Second Order Differential Equation Have Two Solutions?
A second order differential equation can have infinitely many solutions as the arbitrary constants can take any value. We find two linearly independent solutions of a second order differential equation as their combination gives all possible solutions of the equation and finding only one solution does not suffice.
How to Find Particular Solution of Second Order Differential Equation?
The particular solution of a second order differential equation can be determined using the table given below:
| f(x) | yp |
|---|---|
| beax | Aeax |
| axn + (lower order powers of x) | Cnxn + Cn-1xn-1 + ... + C0 |
| P cos ax or Q sin ax | A cos ax + B sin ax |
We can also find the particular solution using the formula yp = -y1 ∫[y2 f(x)/W(y1, y2)] dx + y2 ∫[y1 f(x)/W(y1, y2)] dx, where y1 and y2 are two linearly independent solutions of the homogeneous second order differential equation y'' + py' + qy = 0
How to Tell If a Second Order Differential Equation is Linear?
To tell if a second order differential equation is linear, we can check the degree of the second derivative in the equation. A linear second order differential equation is written as y'' + p(x)y' + q(x)y = f(x), where the power of the second derivative y'' is equal to one which makes the equation linear.
What is the Difference Between First Order Differential Equation and Second Order Differential Equation?
A first-order differential equation consists of the first derivative of a function and no other higher order derivative can appear in the equation. It is written as y' + p(x)y = f(x). On the other hand, second order differential equation is a differential equation that consists of a derivative of a function of order 2 and no other higher-order derivative of the function appears in the equation. It is written as y'' + p(x)y' + q(x)y = f(x).
visual curriculum