Golden Ratio
The golden ratio, which is often referred to as the golden mean, divine proportion, or golden section, is a special attribute, denoted by the symbol ϕ, and is approximately equal to 1.618. The study of many special formations can be done using special sequences like the Fibonacci sequence and attributes like the golden ratio.
This ratio is found in various arts, architecture, and designs. Many admirable pieces of architecture like The Great Pyramid of Egypt, Parthenon, have either been partially or completely designed to reflect the golden ratio in their structure. Great artists like Leonardo Da Vinci used the golden ratio in a few of his masterpieces and it was known as the "Divine Proportion" in the 1500s. Let us learn more about the golden ratio in this lesson.
| 1. | What is the Golden Ratio? |
| 2. | Golden Ratio Formula |
| 3. | How to Calculate the Golden Ratio? |
| 4. | What is Golden Rectangle? |
| 5. | What is the Fibonacci Sequence? |
| 6. | FAQs on Golden Ratio |
What is the Golden Ratio?
The golden ratio, which is also referred to as the golden mean, divine proportion, or golden section, exists between two quantities if their ratio is equal to the ratio of their sum to the larger quantity between the two. With reference to this definition, if we divide a line into two parts, the parts will be in the golden ratio if:
The ratio of the length of the longer part, say "a" to the length of the shorter part, say "b" is equal to the ratio of their sum " (a + b)" to the longer length.
Refer to the following diagram for a better understanding of the above concept:

It is denoted using the Greek letter ϕ, pronounced as "phi". The approximate value of ϕ is equal to 1.61803398875... It finds application in geometry, art, architecture, and other areas. Thus, the following equation establishes the relationship for the calculation of golden ratio: ϕ = a/b = (a + b)/a = 1.61803398875... where a and b are the dimensions of two quantities and a is the larger among the two.
Golden Ratio Definition
When a line is divided into two parts, the long part that is divided by the short part is equal to the whole length divided by the long part is defined as the golden ratio. Mentioned below are the golden ratio in architecture and art examples.
There are many applications of the golden ratio in the field of architecture. Many architectural wonders like the Great Mosque of Kairouan have been built to reflect the golden ratio in their structure. Artists like Leonardo Da Vinci, Raphael, Sandro Botticelli, and Georges Seurat used this as an attribute in their artworks.

Golden Ratio Formula
The Golden ratio formula can be used to calculate the value of the golden ratio. The golden ratio equation is derived to find the general formula to calculate golden ratio.
Golden Ratio Equation
From the definition of the golden ratio,
a/b = (a + b)/a = ϕ
From this equation, we get two equations:
a/b = ϕ → (1)
(a + b)/a = ϕ → (2)
From equation (1),
a/b = ϕ
⇒ a = b
Substitute this in equation (2),
(bϕ + b)/bϕ = ϕ
b( ϕ + 1)/bϕ = ϕ
(ϕ + 1)/ϕ = ϕ
1 + 1/ϕ = ϕ
1 + 1/ϕ = ϕ
How to Calculate the Golden Ratio?
The value of the golden ratio can be calculated using different methods. Let us start with a basic one.
Hit and trial method
We will guess an arbitrary value of the constant, then follow these steps to calculate a closer value in each iteration.
- Calculate the multiplicative inverse of the value you guessed, i.e., 1/value. This value will be our first term.
- Calculate another term by adding 1 to the multiplicative inverse of that value.
- Both the terms obtained in the above steps should be equal. If not, we will repeat the process till we get an approximately equal value for both terms.
- For the second iteration, we will use the assumed value equal to the term 2 obtained in step 2, and so on.
For example,
Since ϕ = 1 + 1/ϕ, it must be greater than 1. Let us start with value 1.5 as our first guess.
- Term 1 = Multiplicative inverse of 1.5 = 1/1.5 = 0.6666...
- Term 2 = Multiplicative inverse of 1.5 + 1 = 0.6666.. + 1 = 1.6666...
Since both the terms are not equal, we will repeat this process again using the assumed value equal to term 2.
The following table gives the data of calculations for all the assumed values until we get the desired equal terms:
| Iteration | Assumed value | Term 1 (1/value) | Term 2 (1/value + 1) |
|---|---|---|---|
| 1. | 1.5 | 11.511.5 = 0.6666.. | 0.6666.. + 1 = 1.6666.. |
| 2. | 1.6666.. | 11.666..11.666.. = 0.6 | 0.6 + 1 = 1.6 |
| 3. | 1.6 | 11.611.6 = 0.625 | 0.625 + 1 = 1.625 |
| 4. | 1.625 | 11.62511.625 = 0.61538.. | 0.61538.. + 1 = 1.61538.. |
| 5. | 1.61538.. | .. | .. and so on |
The more iterations you follow, the closer the approximate value will be to the accurate one. The other methods provide a more efficient way to calculate the accurate value.
Golden Ratio Equation
Another method to calculate the value of the golden ratio is by solving the golden ratio equation.
We know,
ϕ = 1 + 1/ϕ
Multiplying both sides by ϕ,
ϕ2 = ϕ + 1
On rearranging, we get,
ϕ2 - ϕ -1 = 0
The above equation is a quadratic equation and can be solved using quadratic formula:
ϕ = \(\frac{-b \pm \sqrt{ b^2 - 4ac}}{2a}\)
Substituting the values of a = 1, b = -1 and c = -1, we get,
ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)
The solution can be simplified to a positive value giving:
ϕ = 1/2 + √5/2
Note that we are not considering the negative value, as \(\phi\) is the ratio of lengths and it cannot be negative.
Therefore, ϕ = 1/2 + √5/2
What is Golden Rectangle?
In geometry, a golden rectangle is defined as a rectangle whose side lengths are in the golden ratio. The golden rectangle exhibits a very special form of self-similarity. All rectangles that are created by adding or removing a square are golden rectangles as well.
Constructing a Golden Rectangle
We can construct a golden rectangle using the following steps:
- Step 1: First, we will draw a square of 1 unit. On one of its sides, draw a point midway. Now, we will draw a line from this point to a corner of the other side.
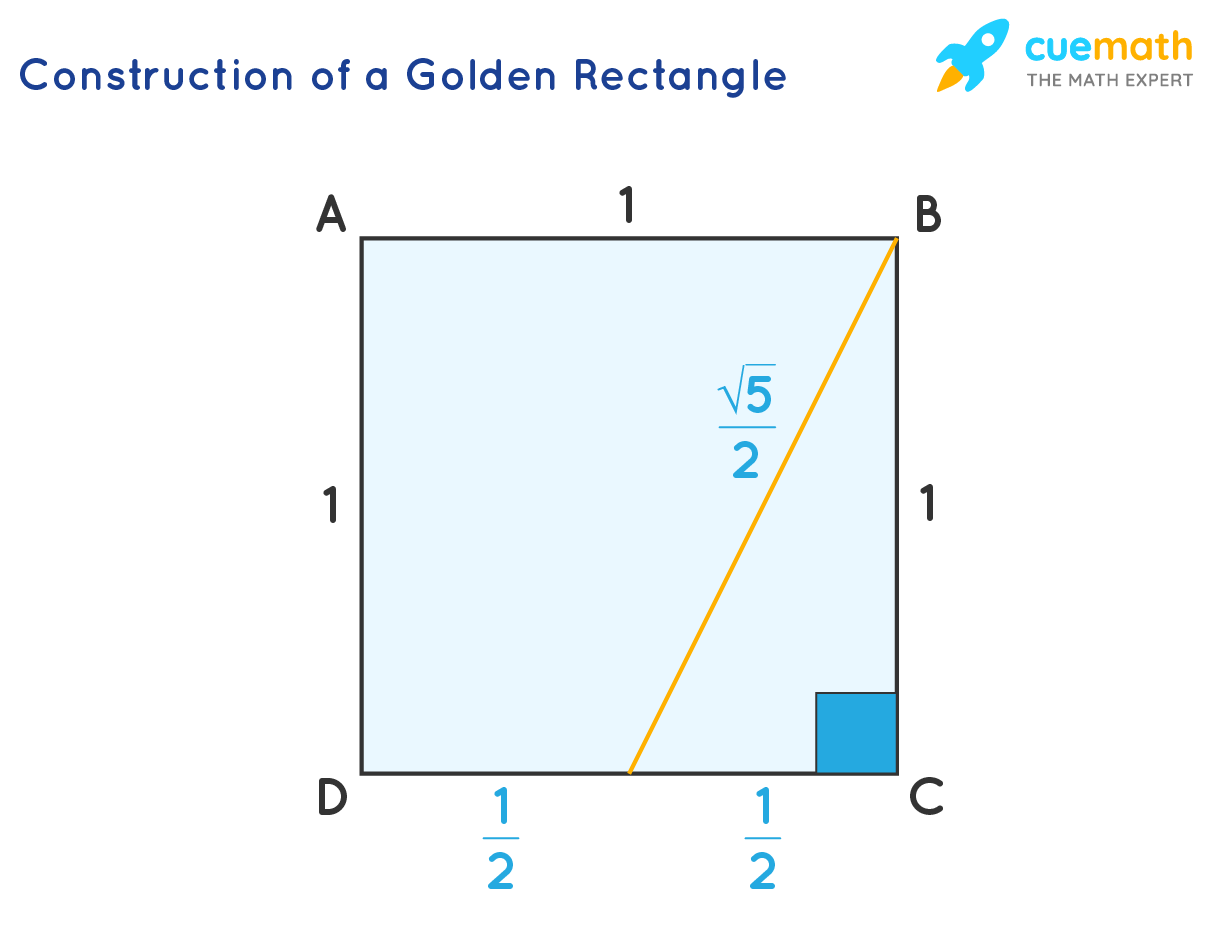
- Step 2: Using this line as a radius and the point drawn midway as the center, draw an arc running along the square's side. The length of this arc can be calculated using Pythagoras Theorem: √(1/2)2 + (1)2 = √5/2 units.
- Step 3: Use the intersection of this arc and the square's side to draw a rectangle as shown in the figure below:

This is a golden rectangle because its dimensions are in the golden ratio. i.e., ϕ = (√5/2 + 1/2)/1 = 1.61803
What is the Fibonacci Sequence?
The Fibonacci sequence is a special series of numbers in which every term (starting from the third term) is the sum of its previous two terms. The following steps can be used to find the Fibonacci sequence:
- We start by taking 0 and 1 as the first two terms.
- The third term 1, is thus calculated by adding 0 and 1.
- Similarly, the next term = 1 + 2 = 3, and so on.
Fibonacci sequence is thus given as, 0, 1, 1, 2, 3, 5, 8, 13, 21,.. and so on. Fibonacci sequence and golden ratio have a special relationship between them. As we start calculating the ratios of two successive terms in a Fibonacci series, the value of every later ratio gets closer to the accurate value of ϕ.
For example,
The following table shows the values of ratios approaching closer approximation to the value of ϕ. The following table shows the values of ratios approaching closer approximation to the value of ϕ.
| Term 1 | Term 2 | Ratio = Term 2/ Term 1 |
|---|---|---|
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6666.. |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 13 | 21 | 1.61538 |
☛Related Topics
Given below is the list of topics that are closely connected to the golden ratio. These topics will also give you a glimpse of how such concepts are covered in Cuemath.
Golden Ratio Examples
-
Example 1: Calculate the value of the golden ratio ϕ using quadratic equations.
Solution:
We know,
ϕ = 1 + 1/ϕ
Multiplying both sides by ϕ,
ϕ2 = ϕ + 1
On rearranging, we get,
ϕ2 - ϕ -1 = 0
The above equation is a quadratic equation and can be solved using quadratic formula:
ϕ = \(\frac{-b \pm \sqrt{ b^2 - 4ac}}{2a}\)
Substituting the values of a = 1, b = -1 and c = -1, we get,
ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)
The solution can be simplified to a positive value giving:
ϕ = 1/2 + √5/2
Note that we are not considering the negative value, as ϕ is the ratio of lengths and it cannot be negative.
Therefore, ϕ = 1/2 + √5/2
-
Example 2: What are the different applications of the golden ratio in our day-to-day lives?
Solution:
The golden ratio is a mathematical ratio, commonly found in nature, and when used in a design, it fosters natural-looking compositions that are pleasing to the eye. There are many applications of the golden ratio in the field of architecture. For example, the Great Pyramid of Egypt and the Great Mosque of Kairouan are a few of the architectural wonders in which the concept of the golden ratio has been used. Artists like Leonardo Da Vinci, Raphael, Sandro Botticelli, and Georges Seurat used this ratio as an attribute in their artworks. It can be used to study the structure of many objects in our daily lives that resemble a certain pattern
-
Example 3: The 14th term in the sequence is 377. Find the next term.
Solution:
We know that 15th term = 14th term × the golden ratio.
\(F_{15}\) = 377 × 1.618034
≈ 609.99 = 610
Therefore, the 15th term in the Fibonacci sequence is 610.

FAQs on Golden Ratio
What is the Golden Ratio in Simple Words?
The golden ratio is a mathematical ratio that exists between two quantities if their ratio is equal to the ratio of their sum to the larger quantity among the two. In other words, when a line is divided into two parts and the longer part 'a' divided by the smaller part 'b', is equal to the sum of (a + b) divided by 'a', this means the line is reflecting the golden ratio, which is equal to 1.618.
What do you Mean by Golden Rectangle?
In geometry, a golden rectangle is defined as a rectangle whose side lengths are in the golden ratio. The golden rectangle exhibits a very special form of self-similarity. All rectangles that are created by adding or removing a square are golden rectangles as well.
Why is the Golden Ratio Beautiful?
The golden ratio is a ratio, which, when used in various fields to design objects, makes the objects aesthetically appealing and pleasing to look at. Therefore, the golden ratio is referred to as a beautiful attribute. It can be noticed in various patterns of nature, like the spiral arrangement of flowers and leaves. There are many applications of the golden ratio in the field of architecture. Many architectural wonders have been built to reflect the golden ratio in their structure, like, the Great Pyramid of Egypt and the Great Mosque of Kairouan.
Why is the Golden Ratio Important?
The golden ratio is a mathematical ratio which is commonly found in nature and is used in various fields. It is used in our day-to-day lives, art, and architecture. Objects designed to reflect the golden ratio in their structure and design are more pleasing and give an aesthetic feel to the eyes. It can be noticed in the spiral arrangement of flowers and leaves.
Where is the Golden Ratio Used in Real Life?
There are many uses of the golden ratio in the field of art and architecture. Many architectural wonders have been built to reflect the golden ratio in their structure. Artists like Leo Da Vinci, Raphael, Sandro Botticelli, and Georges Seurat used this as an attribute in their artworks. It can be used to study the structure of many objects in our daily lives that resemble a certain pattern.
Who Discovered the Golden Ratio?
Ancient Greek mathematicians were the first ones to mention the golden ratio in their work. The 5th-century BC mathematician Hippacus and Euclid contributed a lot of their research work on this subject.
What is Golden Ratio Formula?
The golden ratio formula can be used to calculate the value of the golden ratio. The formula to calculate the golden ratio is given as,
1 + 1/ϕ = ϕ
where ϕ denotes the golden ratio.
visual curriculum