Practical Counting Situations

Situation 1: Suppose that you have to travel from city A to city C, via city B. There are four trains available from A to B (named a, b, c, d), and three trains available from B to C (named p, q, r).

In how many different ways can you travel from A to C? In other words, how many different train combinations exist to travel from A to C?

We note that for each of the four choices of trains from A to B, we have three choices of trains from B to C. Thus, we have \(4 \times 3 = 12\) possible combinations of trains from A to C. These are listed out explicitly below:

\[\begin{align}& ap & aq & & ar\\&bp & bq && br\\&cp & cq && cr\\&dp & dq && dr\end{align}\]

Situation 2: In a class, there are 10 boys and 12 girls. For a school debate, the teacher has to select a pair consisting of a boy and a girl. In how many ways can she do this? In other words, how many options does the teacher have in forming a pair consisting of a boy and a girl?

For any boy that the teacher selects, she has 12 options for selecting the girl in the pair. Since there are 10 boys, and there are 12 options of the girl for each boy, the total number of options to form a boy-girl pair is \(10 \times 12 = 120\).

Situation 3: Ayesha has a set of five letter-blocks: A, B, C, D and E. How many different two-letter words can Ayesha make from these blocks?

Ayesha has five options for the first letter of the word. Once she has selected the first letter, she has four options for the second letter. Thus, she has \(5 \times 4 = 20\) options to form the two letter word. These are listed out explicitly below:

\[\begin{align}&{\rm{AB}} & {\rm{AC}} && {\rm{AD}} && {\rm{AE}}\\&{\rm{BA}} & {\rm{BC}} && {\rm{BD}} && {\rm{BE}}\\&{\rm{CA}} & {\rm{CB}} && {\rm{CD}} && {\rm{CE}}\\&{\rm{DA}} & {\rm{DB}} & &{\rm{DC}} && {\rm{DE}}\\&{\rm{EA}} & {\rm{EB}} & &{\rm{EC}} && {\rm{ED}}\end{align}\]

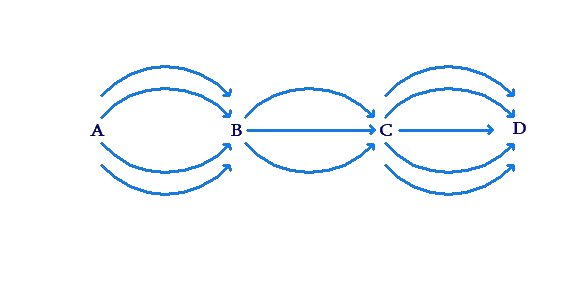
Situation 4: Manan has to travel from city A to city D, via city B and city C. There are five trains available from A to B, three flights available from B to C, and four buses available from C to D:

In how many ways can Manan travel from A to D? In other words, how many different travel combinations exist to get from A to D?

We note there are \({\rm{5}} \times {\rm{3 = 15}}\) ways to get from A to C. For each of these 15 ways to get from A to C, there are four ways to get from C to D. Thus, there are \({\rm{5}} \times {\rm{3}} \times {\rm{4 = 15}} \times {\rm{4 = 60}}\) ways to get from A to D.

Situation 5: There are three sections in Class-9 in a small school. Each section has 10 students. The teacher has to select one student from each section for an inter-school event, in which three students will participate. In how many ways can the teacher make this selection?

Let us name the sections: A, B and C. The teacher can select a pair of students from sections A and B (one from each section) in \(10 \times 10 = 100\) ways. For each of these 100 ways, she can select the third student in 10 ways (from section C). Thus, she can select a triplet of students (one from each section) in \(10 \times 10 \times 10 = 1000\)ways.

Situation 6: Sumedha has four letter blocks: A, B, C and D. How many different three letter words can she make from these blocks?

Sumedha can select the first letter of the word in four ways, and the second letter in three ways. Thus, she can select the first two letters in \(4 \times 3 = 12\) ways. For each of these 12 ways, she has only two options left for the third letter. Thus, she can form a three letter word in \(4 \times 3 \times 2 = 24\) ways. These 24 different possibilities are listed out below (each row lists out all the words starting with one particular letter):

\[\begin{align}&ABC & ABD & &ACB & &ACD && ADB & &ADC\\&BAC & BAD && BCA && BCD & & BDA & & BDC\\ &CAB & CAD &  &CBA & & CBD &  &CDA & & CDB\\ &DAB & DAC & & DBA & & DBC & & DCA & & DCB\end{align}\]

The idea which we have used in the six scenarios above is a very fundamental mathematical principle.

Fundamental Principle of Counting (FPC): If one task can be done in m ways and another task can be done (independently) in n ways, then the two tasks can be done together in \(m \times n\) ways.

This is not a very rigorous definition, as we have not defined the term “independently”. However, it will suffice for now – start thinking of this principle intuitively.

We can extend this principle to more than two tasks. We already did so when we calculated the number of ways to travel from city A to city D via cities B and C. The generalized FPC can be stated as follows.

If task T₁ can be done in n₁ ways, task T₂ can be done in n₂ ways, task T₃ can be done in n₃ ways, and so on, then these tasks together can be done in \({n_1} \times {n_2} \times {n_3} \times ..\) ways.