Angle Sum Property in Quadrilaterals
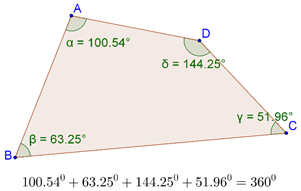
We have seen that in any triangle, the sum of the three angles is 1800. In any quadrilateral, the sum of the four angles is 3600. The following figure shows an example:
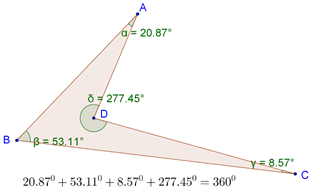
This fact will hold true even if one of the angles of the quadrilaterals is reflex, as shown below:
The justification of the angle sum property is based on the angle sum property of triangles.
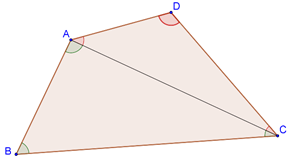
Proof: Consider any quadrilateral ABCD, and draw the diagonal AC, as shown below:
The angles of triangle ABC sum to 1800, and the angles of triangle ADC also sum to 1800. Thus, the total sum of these angles (which is actually equal to the sum of the four angles of the quadrilateral) is 3600. Formally:
In \(\Delta ABC\), we have:
\(\angle ABC\) + \(\angle BCA\) + \(\angle CAB\) = 1800
Similarly, in \(\Delta ADC\), we have:
\(\angle ACD\)+ \(\angle CDA\)+ \(\angle DAC\) = 1800
Summing the two relations, we have:
\(\angle ABC\) + \(\angle CDA\) + (\(\angle BCA\) + \(\angle ACD\)) + (\(\angle CAB\) +\(\angle DAC\)) = 1800
è \(\angle ABC\) + \(\angle CDA\) + \(\angle BCD\) + \(\angle DAB\) = 3600
è\(\angle B\) + \(\angle D\) + \(\angle C\) + \(\angle A\) = 3600