Circles Touching Each Other

Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point.

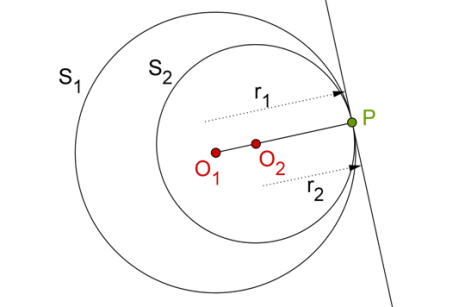
Consider the following figure, where two circles S₁ and S₂ (with radii r₁ and r₂) touch each other externally at P. In this case, the distance between O₁ and O₂ (their centers) is r₁ + r₂ (note that this rests on the fact that the centers and the point of contact are collinear, something we will soon prove):

On the other hand, S₁ and S₂ touch each other internally in the following figure, and the distance between O₁ and O₂ in this case is r₁ – r₂ (r₁ is the larger radius):

Once again, the fact that the distance between the two centers is equal to the difference of the two radii rests on the fact that the centers and the point of contact are collinear. Note the common tangent(s) in both cases, and the following:

• If two circles touch each other externally, the two circles are on opposite sides of their common tangent.

• On the other hand, if two circles touch other internally, the two circles are on the same side of their common tangent.

Theorem: If two circles touch each other (externally or internally), then their point of contact lies on the straight line joining their centers.

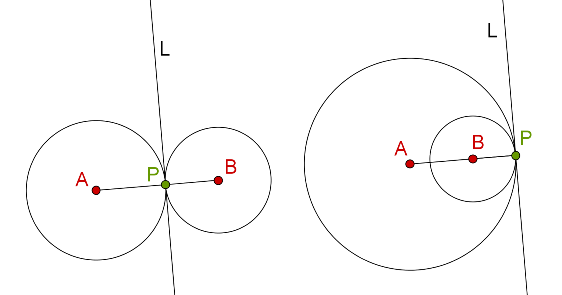
Consider the following figure. On the left side, we have two circles touching each other externally, while on the right side, we have two circles touching each other internally. Note that at the point of contact, a common tangent L can be drawn to both the circles:

Proof: The justification of this result is quite straightforward. In both the cases above, AP must be perpendicular to L, and so must BP. This is because L is the tangent to both the circles at P. Thus, both the perpendiculars AP and BP pass through the same point P, which necessarily implies that A, P and B are collinear. And we can now further derive the following useful result.

Corollary: For two circles touching each other, the distance between their centers is equal to the sum of their radii (if the circles touch each other externally) or the difference of their radii (if the circles touch each other internally).

Justifying this should be obvious by now, and is left to you as an exercise. Make use of the fact that A, P and B are collinear.