Concyclic Points

A set of points is said to be concyclic if a circle passes through all of them. We have already seen that three non-collinear points are always concyclic, because there will always exist a (unique) circle passing through them. The question now is: suppose that there are four points A,B,C and D (any three of which are non-collinear). Will they always be concyclic?

A little thinking will show that the answer is: No. If you draw the circle passing through, for example, A,B and C, it is not at all necessary that this same circle will pass through D as well. Therefore, four points will in general not be concyclic. However, there can be special situations when four points are concyclic. The next theorem discusses one such special situation.

In the figure below, we have four concyclic points on the left, and four non-concyclic points on the right.

Theorem: If the segment joining two points A and B subtends equal angles at two other points C and D on the same side of AB, then the four points are concyclic.

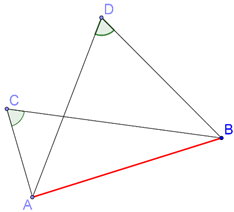
Consider the following figure, which shows how C and D lie on the same side of AB, and that\(\angle {\rm{ACB }} = \angle {\rm{ADB}}\).

Will A, B, C and D be concyclic? Our theorem says: yes.

Proof: Draw the circle passing through A,B and C. Suppose that it does not pass through D. Then, it will intersect AD (or AD extended) at some point, say, E:

In either of the two cases above, we have:

\(\angle {\rm{ACB }} = \angle {\rm{ADB}}\) (given)

\(\angle {\rm{ACB }} = \angle {\rm{AEB}}\) (angles subtended by the same arc AB)

è \(\angle {\rm{ADB }} = \angle {\rm{AEB}}\)

This equality essentially means that in\(\Delta {\rm{BED}}\), an exterior angle is equal to an opposite interior angle. Is that possible? No.

Thus, the circle does pass through D – and hence all the four points A, B, C and D are concyclic.

Example 1: Prove that any four vertices of a regular pentagon are concyclic.

Solution:      Consider the following figure:

We will show that B, C, D and E are concyclic. We note that \(\Delta BCD = \Delta EDC \) (by the SAS criterion), and so, \(\angle {\rm{CBD}}\) =\(\angle {\rm{CED}}\) that is, CD subtends the same angle at B and E. This proves our assertion.