Constructing Perpendicular Bisectors

Suppose that you are given a line segment AB. How can you construct the perpendicular bisector of this segment? Once again, you can use only a straight-edge and a compass. To carry out this construction, we will use the fact that any point on the perpendicular bisector of a line segment is equidistant from the two end-points of the line segment.

The steps in the construction are outlined below.

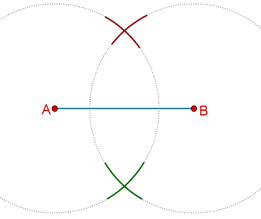
Step 1: Taking A and B as centers, and a radius more than half of AB, draw arcs on both sides of AB, to intersect each other, as shown below.

The reason you require the radius of your arcs to be more than ½ AB is that if the radius is less than ½ AB, the arcs will not intersect (try it!).

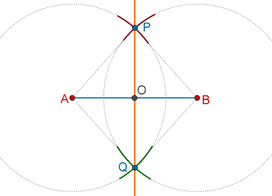
Step 2: Let the two points of intersection so obtained be P and Q. Draw a line through P and Q. This is the required perpendicular bisector.

Let us justify this construction.

Proof: Compare \(\Delta PAQ\) and \(\Delta PBQ\):

1. PA = PB (arcs of equal radii)

2. QA = QB (again, arcs of equal radii)

3. PQ = PQ (common)

By the SSS criterion, the two triangles are congruent, which means that \(\angle APO\) = \(\angle BPO\). Now, compare \(\Delta APO\) with \(\Delta BPO\):

1. PA = PB (arcs of equal radii)

2. \(\angle APO\) = \(\angle BPO\) (just shown)

3. PO = PO (common)

By the SAS criterion, the two triangles are congruent, which means that AO = BO, and also:

\(\angle AOP\) = \(\angle BOP\) = ½ (180⁰) = 90⁰

Clearly, POQ is the perpendicular bisector of AB.