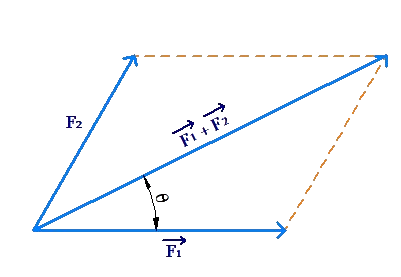
Handling Vectors Specified in the i-j form
Using the \(\widehat i\)- \(\widehat j\)system, it is very easy to add or subtract vectors. Consider the following two vectors:
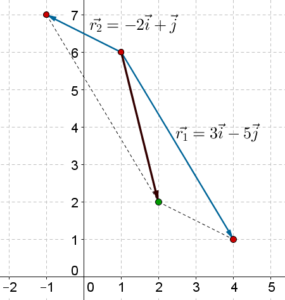
\[\begin{array}{l}\overrightarrow {{r_1}} = 3\widehat i - 5\widehat j\\\overrightarrow {{r_2}} = - 2\widehat i + \widehat j\end{array}\]
What will be the sum of these two vectors? To calculate the sum, we can simply add the \(\widehat i\)components separately, and the \(\widehat j\)components separately. Thus,
\[\begin{array}{l}\overrightarrow {{r_1}} + \overrightarrow {{r_2}} = \left( {3 + \left( { - 2} \right)} \right)\widehat i + \left( {\left( { - 5} \right) + 1} \right)\widehat j\\\,\,\,\,\,\,\,\,\,\,\,\,\,\quad = \widehat i - 4\widehat j\end{array}\]
The correctness of this answer can be verified through the following figure:
Why does this method of separately adding components work? Think in terms of net effects. Suppose that
\[\begin{array}{l}\overrightarrow {{r_1}} = {x_1}\widehat i + {y_1}\widehat j\\\overrightarrow {{r_2}} = {x_2}\widehat i + {y_2}\widehat j\end{array}\]
Now, \(\overrightarrow {{r_1}} + \overrightarrow {{r_2}} \) represents the net effect of \(\overrightarrow {{r_1}} \) and \(\overrightarrow {{r_2}} \). How can we calculate this effect?
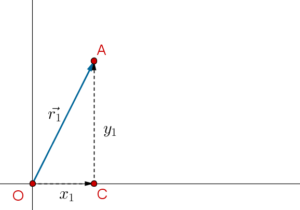
Starting from any point, say, the origin, \(\overrightarrow {{r_1}} \) will take us \({x_1}\) units in the \(\widehat i\)-direction and \({y_1}\) units in the \(\widehat j\)-direction:
Now, if we apply a displacement of \(\overrightarrow {{r_2}} \), this will take us another \({x_2}\) units in the \(\widehat i\)-direction, and \({y_2}\) units in the \(\widehat j\)-direction:
If we now see our net movement in the \(\widehat i\)-direction, it is \(\left( {{x_1} + {x_2}} \right)\), while our net movement in the \(\widehat j\)-direction is \(\left( {{y_1} + {y_2}} \right)\). Thus, the net effect of \(\overrightarrow {{r_1}} + \overrightarrow {{r_2}} \) was to move us \(\left( {{x_1} + {x_2}} \right)\) units in the \(\widehat i\)-direction and \(\left( {{y_1} + {y_2}} \right)\) units in the \(\widehat j\)-direction. This means that
\[\overrightarrow {{r_1}} + \overrightarrow {{r_2}} = \left( {{x_1} + {x_2}} \right)\widehat i + \left( {{y_1} + {y_2}} \right)\widehat j\]
Subtraction works similarly. Suppose that
\[\overrightarrow {{r_1}} - \overrightarrow {{r_2}} = \left( {{x_1} - {x_2}} \right)\widehat i + \left( {{y_1} - {y_2}} \right)\widehat j\]
The \(\widehat i\)-components and the \(\widehat j\)-components can be added separately. Verify this graphically using the following two vectors once again:
\[\begin{array}{l}\overrightarrow {{r_1}} = 3\widehat i - 5\widehat j\\\overrightarrow {{r_2}} = - 2\widehat i + \widehat j\end{array}\]
Example 1: Let \(\overrightarrow a \) and \(\overrightarrow b \) be two vectors such that
\[\begin{array}{l}\overrightarrow a = 4\widehat i - 3\widehat j\\\overrightarrow b = - 2\widehat i + 7\widehat j\end{array}\]
Find the magnitude of \(\left| {\overrightarrow a + \overrightarrow b } \right|\) and \(\left| {\overrightarrow a - \overrightarrow b } \right|\).
Solution: We have:
\[\begin{align}&\overrightarrow a + \overrightarrow b = \left( {4\widehat i - 3\widehat j} \right) + \left( { - 2\widehat i + 7\widehat j} \right)\\\,\,\,\,\,\,\,\,\,\,\, &\qquad\;\;\;\;= \left( {4 + \left( { - 2} \right)} \right)\widehat i + \left( { - 3 + 7} \right)\widehat j\\\,\,\,\,\,\,\,\,\,\,\, &\qquad\;\;\;\;= 2\widehat i + 4\widehat j\\&\overrightarrow a - \overrightarrow b = \left( {4\widehat i - 3\widehat j} \right) - \left( { - 2\widehat i + 7\widehat j} \right)\\\,\,\,\,\,\,\,\,\,\,\, &\qquad\;\;\;\;= \left( {4 - \left( { - 2} \right)} \right)\widehat i + \left( { - 3 - 7} \right)\widehat j\\\,\,\,\,\,\,\,\,\,\,\, &\qquad\;\;\;\;= 6\widehat i - 10\widehat j & \end{align}\]
Thus,
\[\begin{array}{l}\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt {{2^2} + {4^2}} = \sqrt {20} = 2\sqrt 5 \\\left| {\overrightarrow a - \overrightarrow b } \right| = \sqrt {{6^2} + {{\left( { - 10} \right)}^2}} = \sqrt {136} = 4\sqrt {34} \end{array}\]
Example 2: A vector \(\overrightarrow a \) of length 5 units is inclined at an angle of 300 to the horizontal. Another vector \(\overrightarrow b \) of length 8 units is inclined at an angle of 1200 to the horizontal:
Find the following vectors:
- \(\overrightarrow a + \overrightarrow b \)
- \(\overrightarrow a - \overrightarrow b \)
- \(2\overrightarrow a + 3\overrightarrow b \)
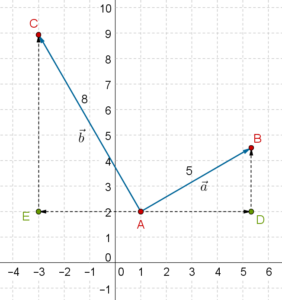
Solution: Let us first specify \(\overrightarrow a \) and \(\overrightarrow b \) in the \(\widehat i\)- \(\widehat j\) system. Consider the following figure:
We have:
\[\begin{array}{l}\overrightarrow a = \overrightarrow {AD} + \overrightarrow {DB} = \left( {5\cos {{30}^0}} \right)\widehat i + \left( {5\sin {{30}^0}} \right)\widehat j\\ \qquad\qquad\quad \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{5\sqrt 3 }}{2}\widehat i + \frac{5}{2}\widehat j\\\overrightarrow b = \overrightarrow {AE} + \overrightarrow {EC} = - \left( {8\cos {{60}^0}} \right)\widehat i + \left( {8\sin {{60}^0}} \right)\widehat j\\ \qquad\qquad\quad \,\,\,\,\,\,\,\,\,\,\,\,\, = - 4\widehat i + 4\sqrt 3 \widehat j\end{array}\]
Thus,
\[\begin{array}{l}\overrightarrow a + \overrightarrow b = \left( {\frac{{5\sqrt 3 }}{2} - 4} \right)\widehat i + \left( {\frac{5}{2} + 4\sqrt 3 } \right)\widehat j\\\overrightarrow a - \overrightarrow b = \left( {\frac{{5\sqrt 3 }}{2} + 4} \right)\widehat i + \left( {\frac{5}{2} - 4\sqrt 3 } \right)\widehat j\\2\overrightarrow a + 3\overrightarrow b = \left( {5\sqrt 3 \widehat i + 5\widehat j} \right) + \left( { - 12\widehat i + 12\sqrt 3 \widehat j} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {5\sqrt 3 - 12} \right)\widehat i + \left( {5 + 12\sqrt 3 } \right)\widehat j\end{array}\]
Example 3: A boy is pulling a box with a force of 10 N towards the east direction. Another boy is pulling the same box with a force of 8 N at an angle of 600 to the east:
If the mass of the box is 4 kg, find its acceleration \(\overrightarrow a \).
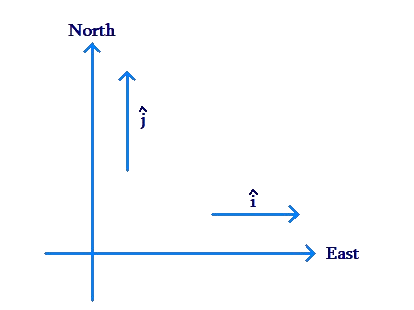
Solution: Note that our answer should be a vector, as the acceleration of the box will have a magnitude as well as a direction. Let us establish an \(\widehat i\)- \(\widehat j\) system such that the \(\widehat i\)-direction is the east direction, while the \(\widehat j\)-direction is the north direction:
Now, if the two forces being applied are represented as \(\overrightarrow {{F_1}} \) and \(\overrightarrow {{F_2}} \), we have:
\[\begin{array}{l}\overrightarrow {{F_1}} = 10\widehat i\,\,\,{\rm{N}}\\\overrightarrow {{F_2}} = \left( {8\cos {{60}^0}} \right)\widehat i + \left( {8\sin {{60}^0}} \right)\widehat j\\\,\,\,\,\,\, = 4\widehat i + 4\sqrt 3 \widehat j\,\,\,{\rm{N}}\end{array}\]
Thus,
\[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = 14\widehat i + 4\sqrt 3 \widehat j\,\,\,{\rm{N}}\]
Clearly, the magnitude of the resultant force is
\[\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {{{14}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = \sqrt {244} \approx 15.6\,\,{\rm{N}}\]
Let \(\theta \) be the inclination of this force with the \(\widehat i\)-direction:
Using the component form of the resultant vector, we can directly write:
\[\begin{align}&\tan \theta = \frac{{4\sqrt 3 }}{{14}} \approx 0.5\\&\Rightarrow \,\,\,\theta \approx {\tan ^{ - 1}}\left( {0.5} \right) \approx {26.5^0} \end{align}\]
The acceleration can be written as
\[\begin{align}&\overrightarrow a = \frac{{\overrightarrow {{F_1}} + \overrightarrow {{F_2}} }}{m} = \frac{{14\widehat i + 4\sqrt 3 \widehat j\,\,\,{\rm{N}}}}{{4\,{\rm{kg}}}}\\ \qquad\quad\;\;\; \,\,\,\,\,\,\,\,\, &\;\;\;\;= 3.5\widehat i + \sqrt 3 \widehat j\,\,\,{\rm{m/}}{{\rm{s}}^2}\end{align}\]
The magnitude of the acceleration is
\[\left| {\overrightarrow a } \right| = \frac{{\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right|}}{m} \approx \frac{{15.6\,\,\,{\rm{N}}}}{{4\,{\rm{kg}}}} \approx 3.9\,{\rm{m/}}{{\rm{s}}^2}\]
The direction of the acceleration is the same as the direction of the net force.
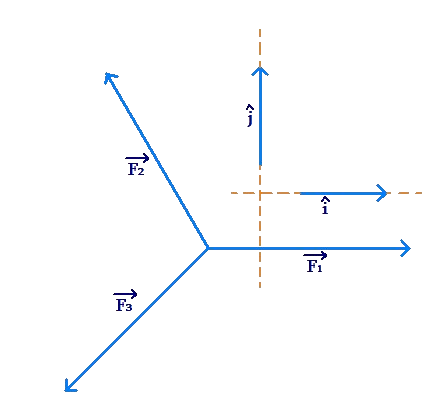
Example 4: Three forces act on a box, as shown in the following figure:
Find the resultant force.
Solution: We take the direction of the first force as the \(\widehat i\)-direction, and the direction perpendicular to it as the \(\widehat j\,\)-direction:
Now, we specify the three forces in this \(\widehat i\, - \,\widehat j\,\)\(\) system (the units are Newtons):
\[\begin{array}{l}\overrightarrow {{F_1}} = 6\widehat i\\\overrightarrow {{F_2}} = \left( {4\cos {{120}^0}} \right)\widehat i + \left( {4\sin {{120}^0}} \right)\widehat j\,\\\,\,\,\,\,\, \;= - 2\widehat i + 2\sqrt 3 \widehat j\,\\\overrightarrow {{F_3}} = \left( {8\cos \left( { - {{150}^0}} \right)} \right)\widehat i + \left( {8\sin \left( { - {{150}^0}} \right)} \right)\widehat j\,\\\,\,\,\,\,\, \;= - 4\sqrt 3 \widehat i - 4\widehat j\,\end{array}\]
The net force will be
\[\begin{align}&\overrightarrow {{F_{net}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \\\,\,\,\,\,\,\,\,\, &\quad\;\;= \left( {6\widehat i} \right) + \left( { - 2\widehat i + 2\sqrt 3 \widehat j} \right) + \left( { - 4\sqrt 3 \widehat i - 4\widehat j} \right)\\\,\,\,\,\,\,\,\,\, &\;\;\;\;\;\;= \left( {4 - 4\sqrt 3 } \right)\widehat i + \left( {2\sqrt 3 - 4} \right)\widehat j\\\,\,\,\,\,\,\,\,\, &\qquad\approx - 2.93\widehat i - 0.54\widehat j\end{align}\]
The magnitude of the net force is
\[\left| {\overrightarrow {{F_{net}}} } \right| \approx \sqrt {{{\left( { - 2.93} \right)}^2} + {{\left( { - 0.54} \right)}^2}} \approx 2.98\,{\rm{N}}\]
If \(\theta \) is the angle of inclination of the net force with the \(\widehat i\)-direction, we have:
\[\theta = - \left( {{{180}^0} - {{\tan }^{ - 1}}\left( {\frac{{0.54}}{{2.93}}} \right)} \right) \approx - {169.5^0}\]
Make sure you understand this last step carefully by drawing an accurate diagram for the net force.