Lines Parallel to the Same Line

Consider a line l, and suppose that we draw two more lines m and n such that l \(\parallel \) m and l \(\parallel \) n.

Can we say that m \(\parallel \) n? Draw any transversal across the three lines, as we have done above, and note that

\(\angle 1\) = \(\angle 2\) (corresponding angles)

\(\angle 2\) = \(\angle 3\) (corresponding angles)

Thus,

\(\angle 1\) = \(\angle 3\)

This proves that m must be parallel to n. We formalize this result in the form of a theorem.

Theorem: Two or more lines which are parallel to the same line will be parallel to each other.

Consider a line l, and consider two more lines m and n such that l \(\parallel \) m and l \(\parallel \) n, as shown below: 

The distance between l and m is x, and the distance between l and n is y. What is the distance between m and n? The theorem above tells us that m and n will also be parallel, and therefore there will be a fixed (constant) distance between them. Clearly, that distance will be x + y.

Example 1: Consider the following figure, in which L₁ and L₂ are parallel lines:

What is the value of \(\angle C\)?

Solution: Through C, draw a line parallel to L₁ and L₂, as shown below:

We have:

\(\angle x\) = \(\angle \beta \) = 60⁰ (alternate interior angles)

\(\angle y\) = 180⁰ – 120⁰ (co-interior angles)

è \(\angle y\) = 60⁰

Thus,

\(\angle C\) = \(\angle x\) + \(\angle y\) = 120⁰

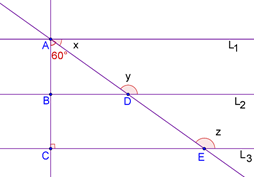
Example 2: Consider the following figure, in which L₁, L₂ and L₃ are parallel lines. The line AC is perpendicular to L₃, as shown:

What are the values of \(\angle x\), \(\angle y\) and \(\angle z\)?

Solution: Since AC ⊥ L₃, it will be perpendicular to each of the other two parallels as well. This means that:

\(\angle x\) = 90⁰ – 60⁰ = 30⁰

Now,

\(\angle y\) = 180⁰ – \(\angle x\) (co-interior angles)

è \(\angle y\) = 150⁰

è \(\angle z\) = \(\angle y\) = 150⁰ (corresponding angles)

Example 3: Consider the following figure, in which L₁ \(\parallel \) L₂:

The angle bisectors of \(\angle BAX\) and \(\angle ABY\) intersect at C, as shown. Prove that \(\angle ACB\) = 90⁰, as indicated in the figure.

Solution: We note that \(\angle BAX\) and \(\angle ABY\) are co-interior angles, which means that their sum is 180⁰:

\(\angle BAX\) + \(\angle ABY\) = 180⁰

è 2(\(\angle 1\) + \(\angle 2\)) = 180⁰

è \(\angle 1\) + \(\angle 2\) = 90⁰

Now, in ΔACB, we apply the angle sum property:

è \(\angle 1\) + \(\angle 2\) + \(\angle ACB\) = 180⁰

è 90⁰ + \(\angle ACB\) = 180⁰

è \(\angle ACB\) = 90⁰

This completes our proof.

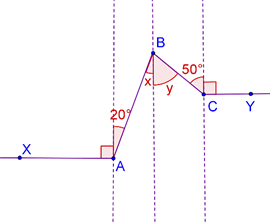
Example 4: Consider the following figure, in which AX \(\parallel \) CY. What is the value of \(\angle B\)?

Solution: Through A and C, drawn two lines perpendicular to AX and CY. Through B, draw a line parallel to these perpendiculars, as shown (the three dotted lines are parallel):

Note how we have marked the various angles. Clearly,

\(\angle x\) = 20⁰ (alternate interior angles)

\(\angle y\) = 50⁰ (alternate interior angles)

Thus,

\(\angle B\) or \(\angle ABC\) = \(\angle x\) + \(\angle y\) = 70⁰.

Example 5: Consider the following figure, in which AX \(\parallel \) DY:

What is the difference between \(\angle 1\) and \(\angle 2\)?

Solution: Through A and D, draw perpendiculars to AX and DY. Through B and C, draw parallels to these perpendiculars, as shown below (note that the four dotted lines are parallel to each other):

Carefully note how we have marked the various angles, using the fact that alternate interior angles for parallel lines are equal. Now, we have:

\(\angle 1\) = \(\angle x\) + 20⁰

\(\angle 2\) = \(\angle x\) + 30⁰

Thus,

\(\angle 2\) – \(\angle 1\) = (\(\angle x\) + 30⁰) – (\(\angle x\) + 20⁰) = 10⁰

Note that this difference is the same as the difference of \(\angle CDY\) and \(\angle BAX\). That is, the actual values of \(\angle B\) and \(\angle D\) have no effect on their difference.

Example 6: Three parallel lines are intersected by a transversal, as shown below:

If \(\angle 1\):\(\angle 2\) = 2:1, what is the value of \(\angle 3\)?

Solution: Consider the following figure:

Clearly, \(\angle 1\) = \(\angle4\), because these are corresponding angles. Now,

\(\angle 1\):\(\angle 2\) = 2:1 è \(\angle4\):\(\angle 2\) = 2:1

Also, \(\angle4\) + \(\angle 2\) = 180⁰, because they are a linear pair. Using these two facts, it is easy to conclude that:

\(\angle4\) = 120⁰, \(\angle 1\) = 60⁰

Thus, \(\angle 1\) = \(\angle4\) = 120⁰, and hence,

\(\angle 3\) = \(\angle 1\) = 120⁰ (alternate interior angles)