Multiplication of a Vector By a Scalar

Consider a vector \(\vec a\). What happens if you multiply this vector by 2? What will the vector \(2\vec a\) represent?

Intuitively, the answer should be clear: the new vector will be twice the length of the original vector, but in the same direction:

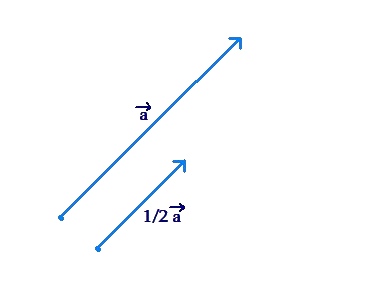
The vector \(\frac{1}{2}\vec a\) will be a vector in the same direction as \(\vec a\), but with a length equal to half of the length of \(\vec a\):

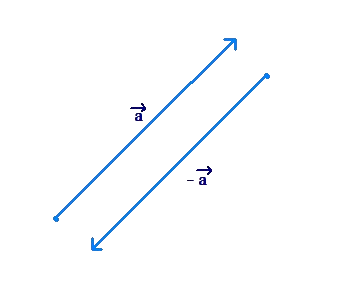
We have seen how to interpret the vector \( - \vec a\), given the vector \(\vec a\):

The two vectors are in opposite directions.

What about the vector \( - 2\vec a\)? The direction of this vector will be opposite to the direction of \(\vec a\), and its length will be twice the length of \(\vec a\):

The vector \( - \frac{1}{2}\vec a\) will have a direction opposite to that of \(\vec a\), and will have a length equal to half the length of \(\vec a\):

To summarize:

• Multiplying a vector by a positive scalar (real number) preserves its direction, and scales its length by the magnitude of the scalar.

• Multiplying a vector by a negative scalar reverses its direction, and scales its length by the magnitude of the scalar.

• It the magnitude of the scalar is greater than 1, then the new vector is longer than the original vector; if it is less than 1, then the new vector is shorter; if the scalar is equal to 1, the new vector has the same length as the original.