Vector Quantities

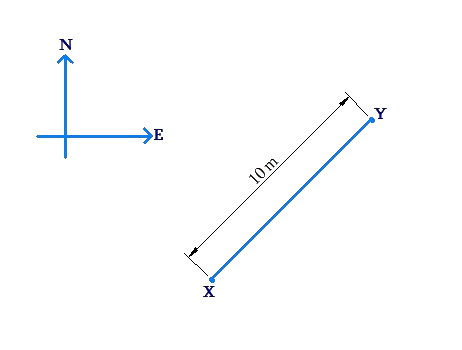
Suppose that from his initial position X, a man walks a distance of 10 meters in the north-east direction to his final position Y, as shown in the figure below:

The displacement of the man is a vector quantity, as it is a quantity which has both a magnitude (10 meters) and a direction (north-east). Without either piece of information, the picture is incomplete. For example, if you are only told that the man walks 10 meters, without specifying the direction of this movement, you will be unable to specify the man’s final position.

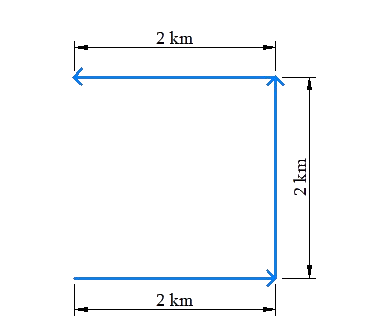
Consider another example. A car travels 2 km towards the east, then 2 km towards the north, and then 2 km towards the west:

The net distance covered by the car is 2 km + 2 km + 2 km = 6 km. However, the net displacement of the car is 2 km north. Observe that:

• The net distance travelled is a quantity which has only a magnitude - it is a scalar quantity.

• The net displacement is a vector quantity - it has both a magnitude and a direction - and it tells us the final position relative to the initial position.

Another example of a vector quantity is velocity. Suppose that a car is initially at some point X, and is moving at a speed of 10 meters / second. Can we specify the position of the car relative to X after, say, 3 seconds? We cannot, unless we know the direction in which the car is moving. If, for example, we are told that the car is moving in the west direction, we can say that after 3 seconds, the position of the car will be 30 meters to the west of X. When you specify the velocity of an object, you specify its speed as well as the direction of its movement (at that instant). Note that speed in itself is a scalar quantity. Speed and direction together becomes velocity - a vector quantity.

Let us consider yet another example of a vector quantity. You have already read about the concept of force, and the fact that force is measured in Newtons. Suppose that you are told that a force of 10 N is applied on a box. This statement tells us only the magnitude of the force, but not its direction. The force will be specified completely only if its direction is also specified. For example, a force of 10 N towards the right:

We have seen three examples of vector quantities, or quantities which require both a magnitude and a direction to be specified completely:

• displacement - a vector quantity which enables us to find the location of the final position relative to the initial position

• velocity - a vector quantity which tells us (at any instant) the speed of an object, as well as its direction of movement

• force - a vector quantity which has not only a magnitude (measured in Newtons) but also a direction in which it is applied

To summarize:

• Scalar quantities have only magnitudes. For example:

  • a distance of 10 meters

  • a speed of 10 meters / second

  • a force of magnitude 10 Newtons

• Vector quantities have both magnitude and direction. For example:

  • a displacement of 10 meters towards the north-east

  • a velocity of 10 meters / second towards the west

  • a force of 10 Newtons towards the right

In this chapter, we will learn how to mathematically deal with vector quantities, or vectors.

A vector is generally represented by a letter with an arrow on top: \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) etc. In the figure below, vector \(\overrightarrow a \) is a vector of magnitude 2 units pointing towards the north, while vector \(\overrightarrow b \) has a magnitude of 3 units and points towards the south-west:

The magnitude of a vector is represented by enclosing it within vertical bars: \(\left| {\overrightarrow a } \right|,\,\left| {\overrightarrow b } \right|,\,\left| {\overrightarrow c } \right|\), etc. For the figure above,

\[\left| {\overrightarrow a } \right| = 2\,{\rm{units,}} \left| {\overrightarrow b } \right| = 3\, {\rm{units}}\]

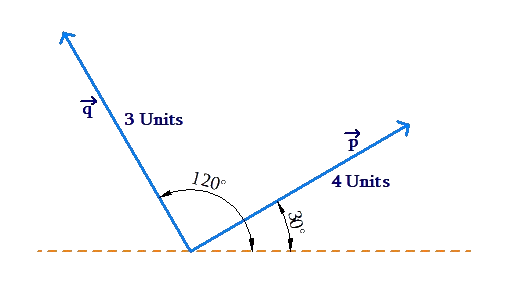
One way to specify the direction of a vector is to specify the angle it makes with a reference direction (say, the x-axis in an x-y coordinate axes system). Consider the following figure, which shows two vectors \(\overrightarrow p \) and \(\overrightarrow q \):

Note that \(\left| {\overrightarrow p } \right|\, = \,4\)  units and \(\left| {\overrightarrow q } \right|\, = \,3\)  units. Also, the direction of \(\overrightarrow p \) is 30° to the horizontal, while the direction of \(\overrightarrow q \) is 120° to the horizontal.

Later on, we will see more succinct ways to specify vector quantities.