Common Chords And Radical Axes

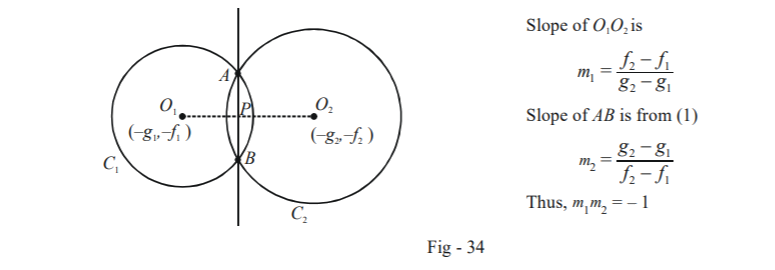
Consider two circles \({C_1}\) and \({C_2}\)  which intersect in two distinct points \(A\) and \(B\). Our purpose is to determine the  equation of \(AB\) which will be termed the common chord of \({C_1}\) and \({C_2}.\)

Let the equations of the circles be

\[\begin{align} {S_1} \equiv {x^2} + {y^2} + 2{g_1}x + 2{f_1}y + {c_1} = 0\\ {S_2} \equiv {x^2} + {y^2} + 2{g_2}x + 2{f_2}y + {c_2} = 0 \end{align}\]

Consider the equation \(S \equiv {S_1} - {S_2} = 0,\) i.e.

\[\begin{align}S \equiv (2{g_1} - 2{g_2})x + (2{f_1} - 2{f_2})y + {c_1} - {c_2} = 0 \qquad \qquad\dots(1)\end{align}\]

Clearly, \(S\) is the equation of a straight line. Observe carefully that since \(A\) and \(B\) lie on both \({C_1}\) and \({C_2}\) , the co-ordinates of \(A\) and \(B\) satisfy both \({S_1}\) and \({S_2}\) and thus \(S \equiv {S_1} - {S_2} = 0.\) This means that \({S_1} - {S_2} = 0\) represents a straight line passing through \(A\) and \(B\). Thus, this is precisely the common chord!

 \(\begin{align}\fbox{$S \equiv {S_1} - {S_2} = 0$}\end{align}\) :  Equation of the common chord

You are urged to observe one important fact about \(S\). It is perpendicular to the line joining the centres of \({C_1}\) and \({C_2};\) this is but expected.

The perpendicularity of \({O_1}{O_2}\) and \(AB\) can be proved geometrically too in a straightforward manner.

The length of the common chord can be easily evaluated using the Pythagoras theorem:

\[AB = 2\sqrt {{O_1}{A^2} - {O_1}{P^2}}  = 2\sqrt {{O_2}{A^2} - {O_2}{P^2}} \]

where \({O_1}P\) and \({O_2}P\)  are the perpendicular distances of \({O_1}\) and \({O_2}\) from the common chord respectively.

Notice an interesting fact: if the length of the common chord \(AB\)  is \(0\), it is actually the common tangent to the two circles \({C_1}\) and \({C_2}\) which will touch each other externally or internally.

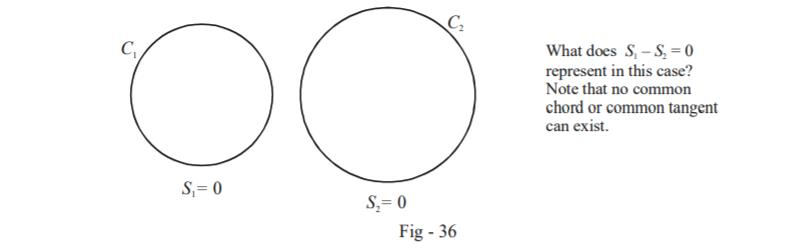
Now an interesting question arises. Suppose that \(C_1\) and \(C_2\) lie external to each other and do not intersect. What does \(S_1 – S_2 = 0\) represent in that case?

\({S_1} - {S_2} = 0\) is obviously a straight line. But it is obviously not a common chord or a common tangent since these do not exist in this case.

The answer is provided by a slight algebraic manipulation. Let a point \(P({x_1},{y_1})\) be such that it satisfies \({S_1} - {S_2} = 0.\) Thus,

\[\begin{align}&{S_1}({x_1},{y_1}) = {S_2}({x_2},{y_1})\\\Rightarrow \qquad  &\sqrt {{S_1}({x_1},{y_1})} = \sqrt {{S_2}({x_1},{y_1})} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\{ \begin{gathered}{\text{Assuming both sides are + ve}}\\{\text{which is true if }}P{\text{ is external }}\\{\rm{to }}\;{C_{\rm{1}}}\;{\rm{ and }}\;{C_2}.\end{gathered} \right\}\end{align}\]

What does this equation tell us? \(P\) is a point such that the lengths of the tangents drawn from it to the two circles are equal. Thus, any point lying on the straight line \({S_1} - {S_2} = 0\) will posess the property that the tangents drawn from it to the two circles are equal. This line is termed the radical axis of the two circles.

It should be obvious that in case of intersecting (or touching) circles, the common chord (or the common tangent) is itself the radical axis. For a situation as in Fig - 37 above, the radical axis exists but no common chord exists. For a circle lying inside another circle, neither the radical axis nor the common chord exist:

Example - 31

Show that the radical axis of three circles, whose centres are non-collinear, taken two \(a + a\) time are concurrent.

Solution: The significance of the phrase ‘non-collinear’ for the three centres should be clear to you: if the centres are all collinear, the three radical axis will become parallel to each other instead of intersecting.

We assume the equations to the three circles to be \({S_1} = 0,\,\,\,{S_2} = 0\) and \({S_3} = 0.\) The three radical axis are therefore

\[\begin{align}{R_1}:{S_1} - {S_2} = 0\\{R_2}:{S_2} - {S_3} = 0\\{R_3}:{S_3} - {S_1} = 0\end{align}\]

Observe that

\[(1){R_1} + (1){R_2} + (1){R_3} = 0\]

which implies that \({R_1},\,\,{R_2}\) and \({R_3}\) are concurrent. The point of concurrency is called the radical centre of the three circles:

Before proceeding we must discuss some properties of two intersecting circles; in particular, we need to understand what we mean by the angle of intersection of two circles.

Consider two intersecting circles \({C_1}\) and \({C_2}\) with radii \({r_1}\) and \({r_2}\) respectively \({O_1}\) and \({O_2}\) centres at and respectively:

The angle of intersection of the two circles can be defined as the angle between the tangents to the two circles at their point(s) of intersection, which will be the same as the angle between the two radii at the point(s) of intersection. In particular, for example, \({C_1}\) and \({C_2}\) in the figure above intersect at an angle \(\angle {O_1}A{O_2}.\)

The most important case we need to consider pertaining to intersecting circles is orthogonal circles, meaning that the angle of intersection of the two circles is a right angle. In that case, the \(\angle {O_1}A{O_2}.\) above will become a right-angled one so that

\[{O_1}{A^2} + {O_2}{A^2} = {O_1}O_2^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...(1)\]

If the two circles and \({C_1}\) and \({C_2}\) have the equations

\[\begin{align}{S_1}:{x^2} + {y^2} + 2{g_1}x + 2{f_1}y + {c_1} = 0\,\,\,;\,\,\,{r_1} = \sqrt {g_1^2 + f_1^2 - {c_1}} \\{S_2}:{x^2} + {y^2} + 2{g_2}x + 2{f_2}y + {c_2} = 0\,\,\,;\,\,\,{r_2} = \sqrt {g_2^2 + f_2^2 - {c_2}} \end{align}\]

then the condition (1) becomes

\[\begin{align}&r_1^2 + r_2^2 = {O_1}O_2^2\\\Rightarrow  \qquad& g_1^2 + f_1^2 - {c_1} + g_2^2 + f_2^2 - {c_2} = {({g_1} - {g_2})^2} + {({f_1} - {f_2})^2}\\\Rightarrow \qquad&  2({g_1}{g_2} + {f_1}{f_2}) = {c_1} + {c_2}\end{align}\]

Thus, the condition that the two circles given by \({S_1}\) and \({S_2}\) must satisfy in order to be orthogonal is

\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\fbox{$2({g_1}{g_2} + {f_1}{f_2}) = {c_1} + {c_2}$}\) : Orthogonal circles

As an exercise, verify that the following pairs of circles intersect orthogonally:

\[\begin{align}\rm{(a)}\qquad &{S_1}:{x^2} + {y^2} - 6x - 8y + 24 = 0\\&{S_2}:{x^2} + {y^2} - 8x - 6y + 24 = 0\\\\\rm{(b)}\qquad &{S_1}:{x^2} + {y^2} + 5x + 3y + 7 = 0\\&{S_2}:{x^2} + {y^2} - 8x + 6y - 18 = 0\end{align}\]

As another example, suppose that we have to find the angle at which

\[\begin{align}{S_1}:{x^2} + {y^2} - 6x + 4y + 11 = 0\\{S_2}:{x^2} + {y^2} - 4x + 6y + 9 = 0\end{align}\]

intersect.

We have,

\[\quad\qquad\qquad\qquad{r_1} = \sqrt 2 ; \qquad   {r_2} = 2; \qquad    {O_1} \equiv (3, - 2);\qquad  {O_2} \equiv (2, - 3)\]

Referring to Fig - 40, let the angle of intersection, \(\angle {O_1}A{O_2}\) be \(\theta \) . By the cosine rule in \(\Delta {O_1}A{O_2},\) we have

\[\begin{align}\cos \theta &= \frac{{r_1^2 + r_2^2 - {O_1}O_2^2}}{{2{r_1}{r_2}}} = \frac{1}{{\sqrt 2 }}\\\Rightarrow\qquad \theta &= \frac{\pi }{4}\end{align}\]

Thus, the two circles intersect at an angle equal to \(\begin{align}\frac{\pi }{4}.\end{align}\)