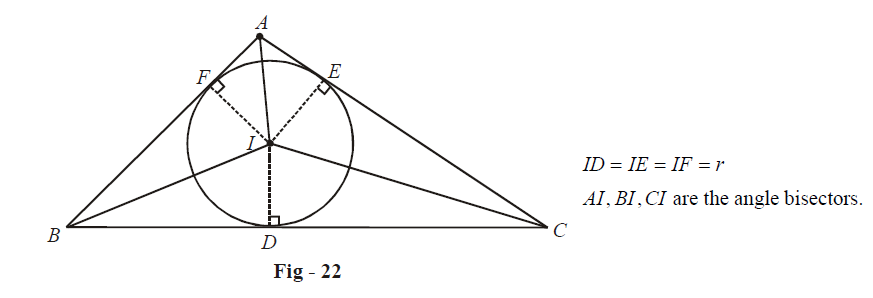Incircle Formulae

The radius of the incircle of a  \(\Delta ABC\)  is generally denoted by r. The incenter is the point of concurrency of the angle bisectors of the angles of   \(\Delta ABC\)  , while the perpendicular distance of the incenter from any side is the radius r of the incircle:

The next four relations are concerned with relating r with the other parameters of the triangle:

\[\boxed{\begin{align}
  & \ r=\frac{\Delta }{s} \\ 
 & \ r=(s-a)\tan \frac{A}{2}=(s-b)\tan \frac{B}{2}=(s-c)\tan \frac{C}{2}\  \\ 
 & \ r=\frac{a\sin \frac{B}{2}\sin \frac{C}{2}}{\cos \frac{A}{2}}=\frac{b\sin \frac{C}{2}\sin \frac{A}{2}}{\cos \frac{B}{2}}=\frac{c\sin \frac{A}{2}\sin \frac{B}{2}}{\cos \frac{C}{2}}\  \\ 
 & \ r=4\ R\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2} \\ 
\end{align}}\]

Proofs: The first of these relations is very easy to prove:

\[\begin{align}&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Delta  = {\text{area}}\;(\Delta BIC) + {\text{area}}\;(\Delta CIA) + {\text{area}}\,(\Delta AIB) \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\quad\quad= \frac{1}{2}ar + \frac{1}{2}br + \frac{1}{2}cr\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\text{How?}}} \right) \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\quad\quad= sr  \\   &\quad\Rightarrow\quad  r = \frac{\Delta }{s} \\ \end{align} \]

To prove the second relation, we note that   \(AE=AF,BD=BF\,\,and\,\,CD=CE\) . Thus,

From  \(\Delta AIE,\)  we have

\[\begin{align}&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tan \frac{A}{2} = \frac{r}{{AE}} = \frac{r}{{s - a}}  \\   &\Rightarrow\quad r = (s - a)\tan \frac{A}{2}  \\\end{align} \]

Similarly, we’ll have \(\begin{align} r = (s - b)\tan \frac{B}{2} = (s - c)\tan \frac{C}{2}\end{align}\)

To prove the third relation, we have

\[\begin{align}&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a = BD + CD  \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\quad\;= \frac{r}{{\tan \frac{B}{2}}} + \frac{r}{{\tan \frac{C}{2}}}  \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\quad\;= \frac{{r\sin \left( {\frac{{B + C}}{2}} \right)}}{{\sin \frac{B}{2}\sin \frac{C}{2}}}  \\  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, &\qquad\quad\;= \frac{{r\cos \frac{A}{2}}}{{\sin \frac{B}{2}\sin \frac{C}{2}}}\qquad{(How?)} \\   &\Rightarrow\quad   r = \frac{{a\sin \frac{B}{2}\sin \frac{C}{2}}}{{\cos \frac{A}{2}}}  \\ \end{align} \]

The other relations follow similarly.

The fourth relation follows from the third and the fact that \(a = 2R\sin A\)  :

\[\begin{align}  r = \frac{{(2R\sin A)\sin \frac{B}{2}\sin \frac{C}{2}}}{{\cos \frac{A}{2}}} \\  \,\,\, = 4R\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}  \\ \end{align} \]