A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Area of Kite

Area of kite is the space enclosed by a kite. A kite is a quadrilateral in which two pairs of adjacent sides are equal. The elements of a kite are its 4 angles, its 4 sides, and 2 diagonals. In this article, we will focus on the area of a kite and its formula.

1. What is the Area of a Kite?
2. Area of a Kite Formula
3. Derivation of the Area of Kite Formula
4. FAQ's on Area of a Kite

What is the Area of a Kite?

The area of a kite can be defined as the amount of space enclosed or encompassed by a kite in a two-dimensional plane. Like a square, and a rhombus, a kite does not have all four sides equal. The area of a kite is always expressed in terms of units2 for example, in2, cm2, m2, etc. Let us learn about the area of a kite formula in our next section.

Area of a Kite Formula

The area of a kite is half the product of the lengths of its diagonals. The formula to determine the area of a kite is: Area = ½ × (d)1 × (d)2. Here (d)1 and (d)2 are long and short diagonals of a kite.
The area of kite ABCD given below is ½ × AC × BD.

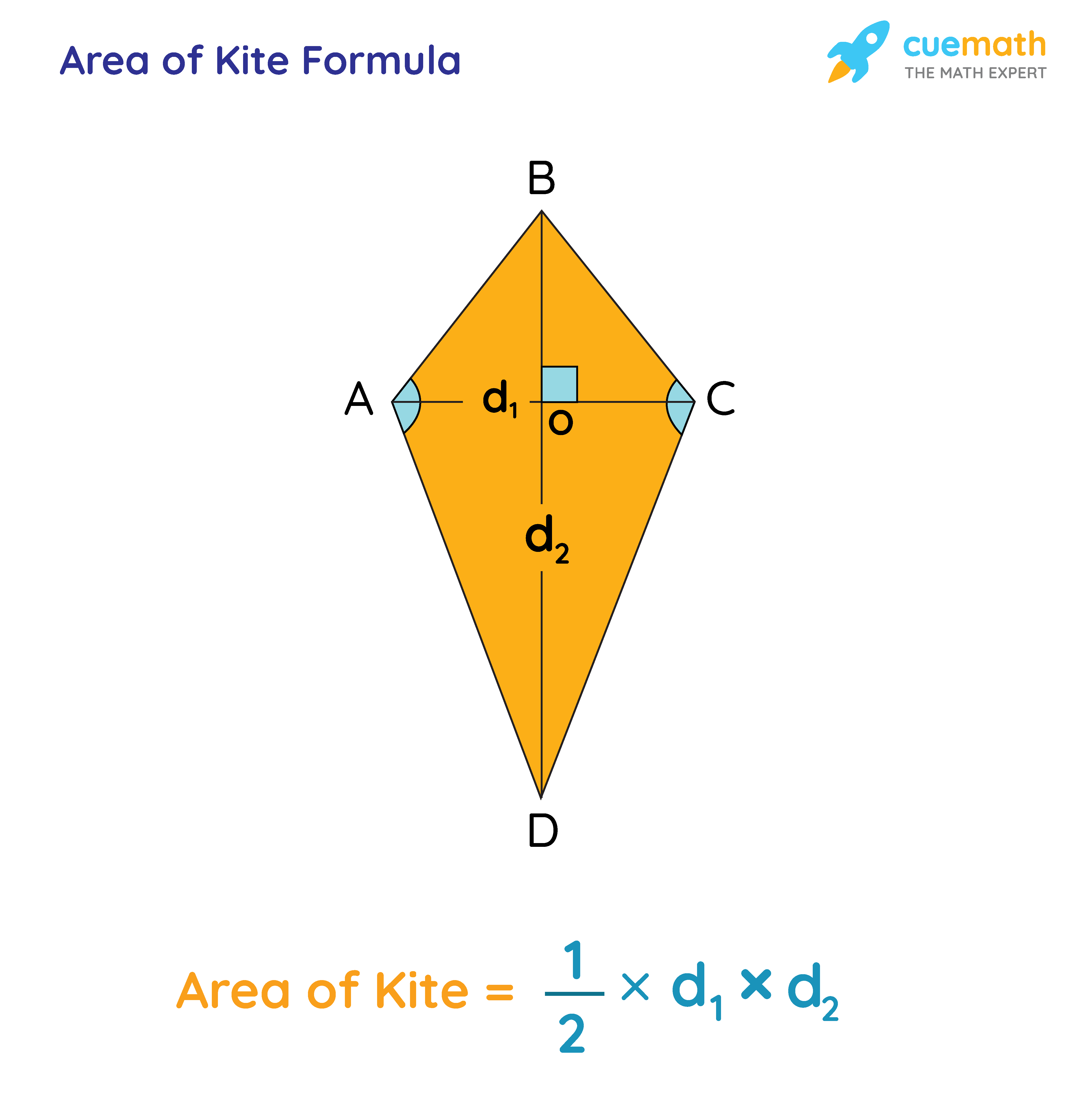
Area of Kite

BD = Long diagonal and AC = Short diagonal

Derivation of the Area of Kite Formula

Consider a kite ABCD as shown above.

Assume the lengths of the diagonals of ABCD to be AC = p, BD = q

We know that the longer diagonal of a kite bisects the shorter diagonal at right angles, i.e., BD bisects AC and ∠AOB = 90°, ∠BOC = 90°.

Therefore,

AO = OC = AC/2 = p/2

Area of kite ABCD = Area of ΔABD + Area of ΔBCD...(1)

We know that,

Area of a triangle = ½ × Base × Height

Now, we will calculate the areas of triangles ABD and BCD

Area of ΔABD = ½ × AO × BD = ½ × p/2 × q = (pq)/4

Area of ΔBCD = ½ × OC × BD = ½ × p/2 × q = (pq)/4

Therefore, using (1)

Area of kite ABCD = (pq)/4 + (pq)/4
= (pq)/2
Substituting the values of p and q
Area of a kite = ½ × AC × BD

Important Notes

  • The perimeter of a kite is \(2(Side_1 + Side_2)\)
  • The area of a kite is ½ × (d)1 × (d)2
  • A kite has two pairs of adjacent equal sides.
  • A kite is a cyclic quadrilateral, hence, satisfies all the properties of a cyclic quadrilateral.
 

Area of Kite Examples

  1. Example 1: Four friends are flying kites of the same size in a park. The lengths of diagonals of each kite are 12 in and 15 in. Determine the sum of areas of all the four kites.

    Solution:

    Lengths of diagonals are:

    (d)1 =12in

    (d)2 =15in

    The area of each kite is:

    A = ½ × (d)1 × (d)2
    = ½ × 12 × 15
    = 90 in2

    Since each kite is of the same size, therefore the total area of all the four kites is 4 × 90 = 360in2.
    Therefore the area of the four kites is 360in2

  2. Example 2: Kate wants to give a kite-shaped chocolate box to her friend. She wants to paste a picture of herself with her friend to cover the top of the box. Determine the area of the top of the box if the diagonals of the lid of the box are 9 in and 12 in.

    Solution:

    (d)1 = 9in

    (d)2 = 12in

    Since the box is kite-shaped, therefore the area of the top of the box is:

    A = ½ × (d)1 × (d)2
    = ½ × 9 × 12
    Therefore, the area of the top of the box is 54in2

  3. Example 3: Find the area of a kite if its diagonals are of the length 12 units and 5 units respectively.

    Solution: The area of a kite can be calculated if the length of its diagonals is known. So, Area of a kite = 1/2 × diagonal 1 × diagonal 2. After substituting the values we get, Area of a kite = 1/2 × 12 × 5 = 30 unit2

Show Answer >

go to slidego to slide

Have questions on basic mathematical concepts?
Become a problem-solving champ using logic, not rules. Learn the why behind math with our Cuemath’s certified experts.

Book a Free Trial Class

FAQs on Area of Kite

How to Find the Area of a Kite?

The area of a kite can be calculated using the formula Area = ½ × (d)1 × (d)2

How to Find the Diagonals of a Kite?

The length of one diagonal of a kite can be found using the Pythagorean theorem. The length of the other diagonal can be found by substituting the length of the first diagonal into the area of a kite formula if the area is known.

What is the Formula of Area of the Kite?

The area of a kite is half the product of the lengths of its diagonals. The formula of area of a kite is given as Area = ½ × (d)1 × (d)2. Here (d)1 and (d)2 are long and short diagonals of a kite.

The area of any kite let's say ABCD with diagonal AC and BD is given as ½ × AC × BD.

What Happens to the Area of Kite If the One Diagonal of Kite is Doubled?

The area of a kite depends on the two diagonals of the kite and is directly proportional. Let us substitute the value of any 1 diagonal as 2(d)1 in the area of the kite formula. The final result we have, A' =½ × 2(d)1 × (d)2. Thus, only the final value of the area of the kite will remain a product of (d)1 and (d)2. This means it will double the value of the area of the kite.

Download FREE Study Materials
Worksheets on Area
Math worksheets and
visual curriculum