Lateral Surface Area of a Cube
The lateral surface area of a cube is defined as the total area of the side faces of the cube. A cube is a three-dimensional shape that is made up of 6 congruent square faces. All the 6 square faces of the cube are of the same size. A cube is referred to as:
- A regular hexahedron (as it has 6 congruent faces) and
- A square prism (as its top and bottom faces are squares)
It is to be noted that a cube is one of the 5 platonic solids. Some real-life examples of a cube are a Rubik's cube, a dice (whose faces are squares), an ice cube, etc. Let us learn what is the lateral surface area of a cube along with the formula, a few solved examples, and practice questions here.
| 1. | What is the Formula for Lateral Surface Area of a Cube? |
| 2. | How to Find the Lateral Surface Area of a Cube? |
| 3. | Lateral Surface Area of a Cube with Diagonal |
| 4. | FAQs on Lateral Surface Area of Cube |
What is the Formula for Lateral Surface Area of a Cube?
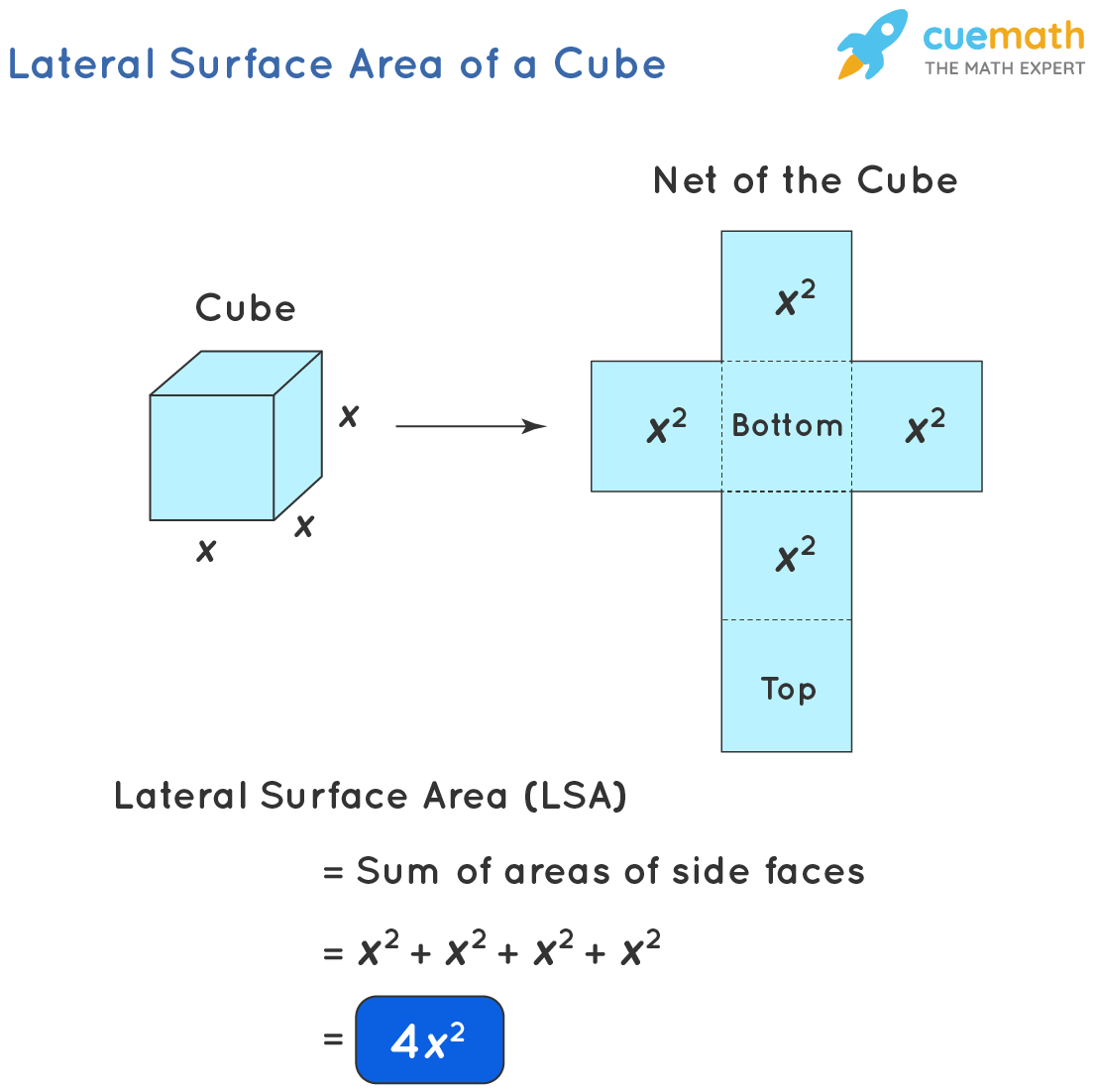
'Lateral' means 'which belongs to the side'. So, the lateral surface area of a cube is the sum of the areas of all side faces of the cube. Can you guess how many side faces does a cube have? Yes, there are 4 side faces (because there are 6 faces in total, among which if we remove the top and the bottom faces, there are only 4 side faces). So the sum of areas of all 4 side faces of a cube is its lateral area. The lateral surface area (LSA) of a cube is also known as its lateral area. The lateral surface area is expressed in square units.
How to Find the Lateral Surface Area of a Cube?
Let us consider a cube of edge length 'x'. As each of its faces is a square, the area of each face = x2 square units. Thus,
The lateral surface area (LSA) of the cube = sum of areas of all 4 side faces
⇒ LSA of cube = x2 + x2 + x2 + x2 = 4x2
Thus, the formula to find the lateral surface area of a cube is, LSA = 4x2
We can understand this formula better using the net of the cube.
Lateral Surface Area of a Cube with Diagonal
In order to find the lateral area of a cube when the space diagonal is given, we need to recall the relationship between the edge length (x) and the space diagonal (d) of a cube. The relationship between the side length (x) and the space diagonal (d) of a cube is expressed as, d = x √3 ⇒ x = d / √3
Substituting this in the formula of the lateral surface area of the cube,
LSA = 4x2 = 4 (d / √3)2 = 4d2 / 3
Thus, the LSA of a cube when its diagonal (d) is given = 4d2 / 3.
We learned that the lateral area of a cube of edge length 'x' is 4x2 and the lateral area of a cube of space diagonal 'd' is 4d2 / 3.
☛ Related Articles
FAQs on Lateral Surface Area of a Cube
What is the Lateral Surface Area of a Cube?
The Lateral Surface Area (LSA) of a cube refers to the area of all the lateral sides of a cube. This is also known as the Lateral Area. There are a total of 4 lateral faces in a cube. So, to find the LSA of a cube, we find the area of 4 of its faces.
What is the Formula for the Lateral Area of a Cube?
We can calculate the lateral area of a cube using the length of each side. The formula that is used to calculate the lateral area of a cube is expressed as, LSA of cube = 4x2, where 'x' is the length of its edge (side).
How to Find the Lateral Surface Area of a Cube?
The lateral surface area of a cube can be obtained by adding the areas of 4 side faces. Thus, the lateral area of the cube = x2 + x2 + x2 + x2 = 4x2. Here 'x' is the length of its side.
What is the Difference Between the Surface Area and Lateral Area of a Cube?
The surface area (or) total surface area (TSA) of a cube is the sum of the areas of all 6 faces whereas the lateral surface area (LSA) is only the sum of the 4 side faces of the cube. If x is the edge length of the cube, then
- Total Surface Area (TSA) = 6x2
- Lateral Surface Area (LSA) = 4x2
How to Find the Side Length of a Cube Using the Lateral Surface Area of Cube?
The side length of a cube can be calculated using the lateral surface area. The formula for the lateral area of a cube is expressed as, 4x2, where 'x' is the side length. Substituting the known value of LSA in this formula, we can find the length of the side of a cube.
How to Find the Lateral Surface Area of a Cube Using the Diagonal?
The lateral surface area of a cube can be calculated if the length of the diagonal is given. The formula to calculate LSA, in this case, is given as, LSA = 4d2 / 3, where 'd' is the space diagonal of the cube.
What is the Lateral Surface Area of a Cube with Side Length 9 cm?
The formula which is used to find the lateral surface area of a cube is Lateral Surface Area (LSA) = 4x2, where 'x' is the side length of the cube. After substituting the value of x = 9 cm, we will get, LSA = 4x2 = 4 × 92 = 324 cm2.