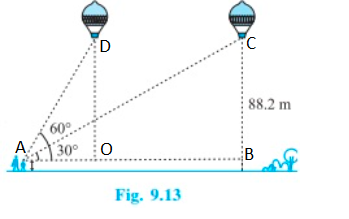
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval
Solution:
Trigonometric ratio involving AB, BC, OD, OA and angles is tanθ. [Refer AB, BC, OA and OD from the figure.]
Distance travelled by the balloon OB = AB - OA
From the figure, OD = BC, and it can be calculated as
88.2 m - 1.2 m = 87 m --- (1)
In ΔAOD,
tan 60° = OD/OA
√3 = 87/OA
OA = 87 / √3
= 87 × √3 / √3 × √3
= (87 × √3) / 3
= 29√3 m
In ΔABC,
tan 30° = BC/AB
1/√3 = 87 / AB
AB = 87√3
Distance travelled by the balloon, OB = AB - OA
OB = 87√3 - 29√3
= 58√3
Distance travelled by the balloon = 58√3 m.
☛ Check: NCERT Solutions Class 10 Maths Chapter 9
Video Solution:
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval
Maths NCERT Solutions Class 10 Chapter 9 Exercise 9.1 Question 14
Summary:
If a 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground and the angle of elevation of the balloon from the eyes of the girl at any instant is 60° and after some time, the angle of elevation reduces to 30°, then the distance travelled by the balloon during the interval is 58√3 m.
☛ Related Questions:
- A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).
- A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
- A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children she wants to have a steep slide at a height of 3m and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
- The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
visual curriculum