A day full of math games & activities. Find one near you.

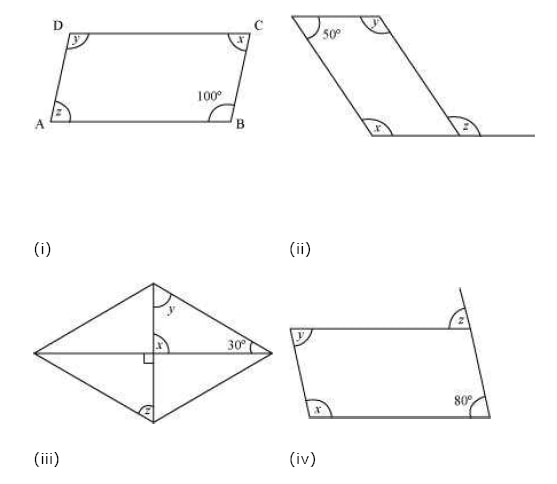
Consider the following parallelograms. Find the values of the unknowns x, y, z.

Solution:

(i) Since ∠D is opposite to ∠B, so, y = 100° (Opposite angles of a parallelogram are equal)

∠C + ∠B = 180° (The adjacent angles in a parallelogram are supplementary)

x + 100° = 180° (The adjacent angles in a parallelogram are supplementary)

Therefore,

x = 180° - 100° = 80°

x = z = 80° (Since opposite angles of a parallelogram are equal)

Thus, x = 80°, y = 100°, z = 80°

(ii) x + 50° = 180° (The adjacent angles in a parallelogram are supplementary)

x = 180° - 50°

= 130°

x = y = 130° (Since opposite angles of a parallelogram are equal)

x = z = 130° (Corresponding angles)

Thus, x = y = z = 130°

(iii) x + y + 30° = 180°(Angle sum property of a triangle)

x = 90° (Vertically opposite angle)

90° + y + 30° = 180°

y + 120° = 180°

y = 60°

z = y = 60° (Alternate interior angles are equal)

x = 90°, y = z = 60°

(iv) z = 80°(Corresponding angles)

y = 80° (Since opposite angles of a parallelogram are equal)

x + y = 180°(Adjacent angles of a parallelogram are supplementary)

x + 80° = 180°

x = 180° - 80°

x = 100°

Thus, x = 100°, y = 80°, z = 80°

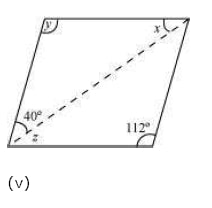
(v) y = 112°(Since opposite angles of a parallelogram are equal)

x + y + 40° = 180° (Angle sum property of a triangle)

x + 112° + 40° = 180°

x + 152° = 180°

x = 180° - 152°

x = 28°

z = x = 28°(Alternate interior angles)

Thus, x = 28°, y = 112°, z = 28°

☛ Check: NCERT Solutions for Class 8 Maths Chapter 3

Video Solution:

Consider the following parallelograms. Find the values of the unknowns x, y, z

NCERT Solutions Class 8 Maths Chapter 3 Exercise 3.3 Question 2

Summary:

In the following parallelograms, the values of the unknowns x, y, z are: (i) The values of x, y and z are 80°, 100° and 80° respectively. (ii) The values of x, y and z are 130°, 130° and 130° respectively. (iii) The values of x, y and z are 90°, 60° and 60° respectively. (iv) The values of x, y and z are 100°, 80° and 80° respectively. (v) The values of x, y and z are 28°, 112° and 28° respectively.

☛ Related Questions: