Decimals and Fractions
A decimal number system is used to express the whole number and fraction together. Here, we will separate the whole number from the fraction by inserting a ".", which is called a decimal point. And a fraction represents a value in the form of a/b. There is a close relationship between decimals and fractions. To convert any decimal number to a fraction, we ignore the decimal point and divide the number by the place value of the last digit in the fractional part of the number. Then we simplify the fraction so obtained. The decimals and fractions can be conveniently interchanged to each other.
The decimals and fractions vary in the format in which they are written. A decimal of 3.24 is written in the form of a fraction of 324/100. In this mini-lesson, we will explore the relationship between decimals and fractions, and understand how to convert a decimal to a fraction.
| 1. | What are Decimals? |
| 2. | Visualizing Decimal Numbers |
| 3. | Decimals and Fractions |
| 4. | Decimals and Percentages |
| 5. | Decimals in Everyday Life |
| 6. | FAQs on Decimals and Fractions |
What are Decimals?
Decimals are a set of numbers written together with a dot in between them that is called a decimal point. The numbers to the left of the decimal point are the integers or whole numbers and the numbers to the right of the decimal point are called decimal numbers. It is very important to understand place value while dealing with comparing decimals, operations on decimals, etc. This is how the place value chart of a decimal number looks like.
In the case of decimals, for the whole number part, the place value system is the same as the whole number. But after the decimal point, there is a different world of numbers going on in which we use decimal fractions to represent the value. When we are going towards the left, each place is ten times greater than the previous place digit. So, to the right of one's place, we have tenths (1/10) and to the right of tenths, we have hundredths (1/100) and so on. Let us look at some examples for more clarity.
| Thousands | Hundreds | Tens | Ones |
Decimal Point |
Tenths | Hundredths | Thousandths | Numbers |
|---|---|---|---|---|---|---|---|---|
| 6 | 7 | 3 | . | 7 | 8 | 9 | 673.89 | |
| 1 | 0 | 7 | 8 | . | 3 | 5 | 0 | 1078.350 |
| 4 | 5 | . | 0 | 8 | 45.08 |
The second way is to read the whole number part followed by "and", then to read the fractional part in the same way as we read whole numbers but followed by the place value of the last digit. For example, we read 34.56 as thirty-four and fifty-six hundredths.
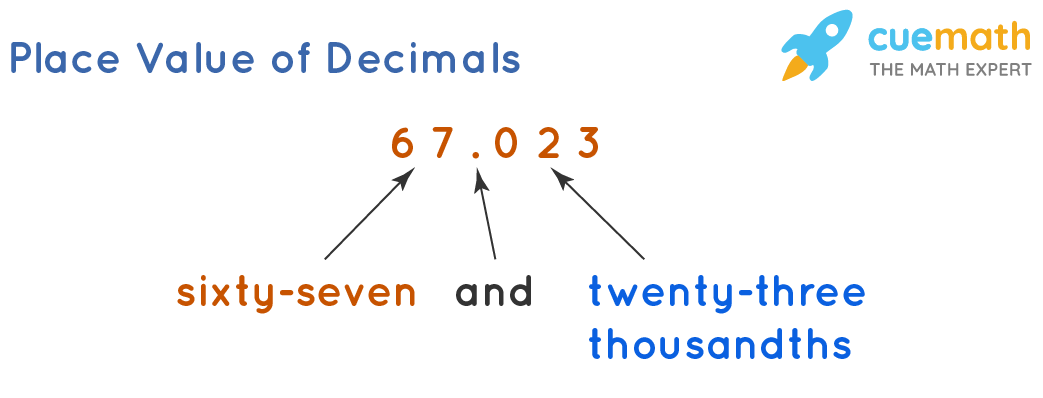
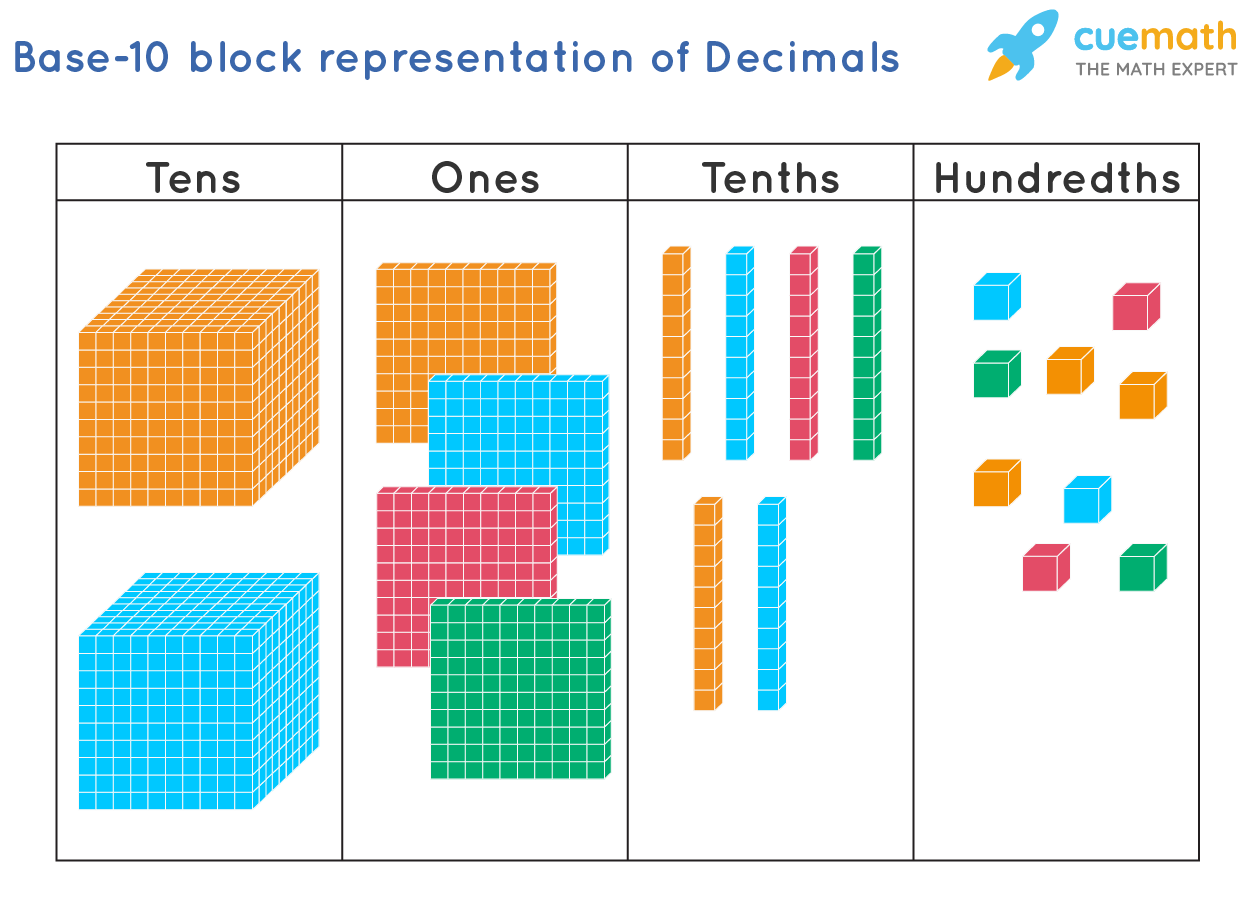
Visualizing Decimal Numbers
We can represent decimal numbers using Base-10 blocks (flats, rods, and blocks). A flat represents one whole unit, a rod one-tenth of the whole, and a block one-hundredth of the whole. So, if want to visualize the number 24.69, it means we have 24 whole units, that we can further represent in the form of 2 cubes and 4 flats; 6 rods (represents tenths) and 9 blocks (represents hundredths).
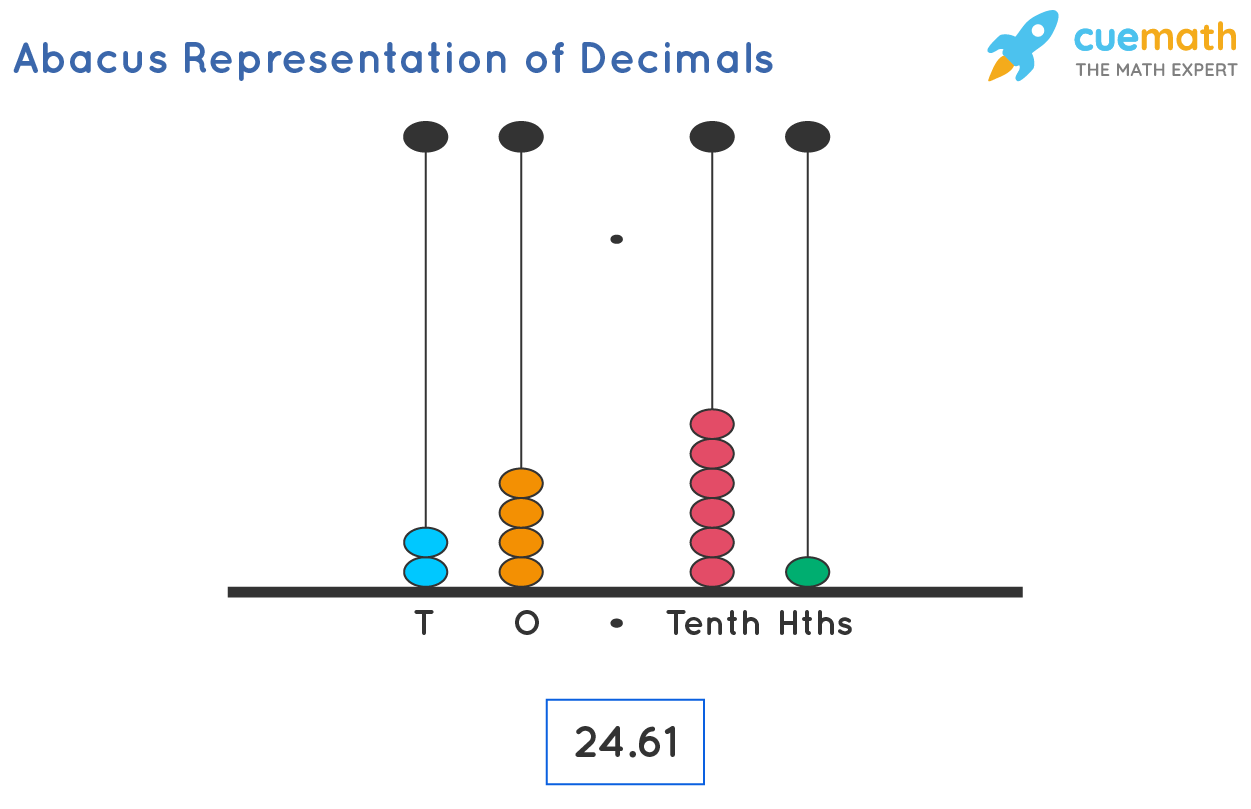
Another way of representing decimal numbers is on the abacus.
Decimals and Fractions
Every decimal number can be expressed in the form of a fraction. There are two simple steps to convert a decimal to fraction. First ignore the decimal and write the entire number with power of 10 based on the number of decimal places. For a decimal number 0.35, write it as 35/100 Further reduce the fraction in its simplest form 35/100 = 7/20. A recurring decimal can also be written as a fraction. A decimal 0.333 can be written as 1/3. Practically many of the decimal numbers can be easily transformed into a fraction. Let us look at one more example for deeper understanding.
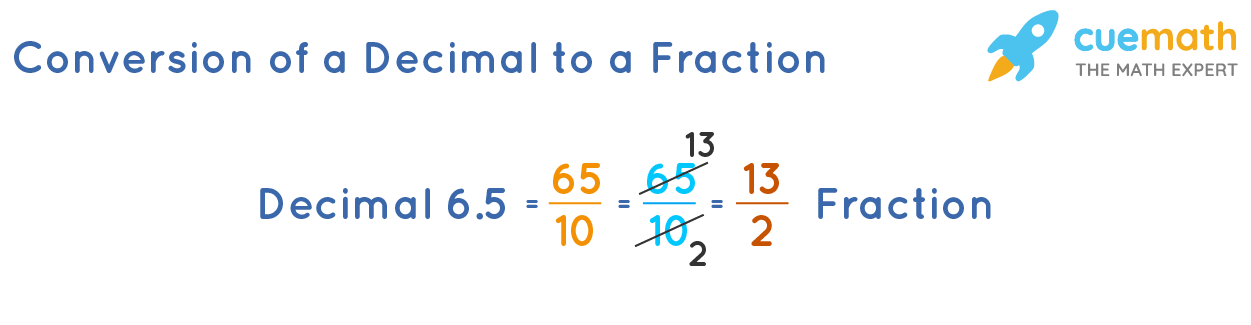
Similarly, we can convert a fraction to its decimal form by the two following methods. There are two methods to convert a fraction into a decimal. The first method is through long division and another method is through multiply the numerator and denominator of the fraction to obtain multiples of 10 like 10, 100, 1000, etc.
Decimals and Percentages
Like fractions, every decimal number can be expressed in the form of a percentage. There is a need to convert decimals to percentages when we compare two or more numbers. For example, who scored better if Sandra got 20.5 out of 40 and Kim got 22.25 out of 45 marks? The process to convert a decimal to a percentage, is through two simple steps. First, multiply the given decimal number with hundred and this moves the decimal by two places towards the right. Further, attach a percentage symbol(%).
For example, 0.67 = 0.67 x 100% = 67%
Similarly, we can convert a percentage to a decimal. First, divide the given percentage number with 100 and remove the decimal symbol. Further simplify the fraction with the 100 in the denominator, to a decimal.
Decimals in Everyday Life
There is a great significance of decimals in everyday life while calculating exact values of money, weight, temperature, length, distance, etc. With the help of decimals, we can represent a part of a unit. Also, very small numeric values can be expressed as a decimal. Examples of a decimal are 0.33387, 0.4897, 0.3398, 0.00001, 0.4597,..... Also, we can say that for counting we need whole numbers but for measuring we need decimals.
Further, we need decimals to be more precise in our calculations in everyday life. For example, Can you fit a table of size 80.3 inches in the given space of 80 inches? The answer for this would be a clear NO. Casually, we say that \(80.3\) is approximately equal to \(80\). But, here, we need to consider the exact measurement in terms of decimal, i.e., 80.3 inches.
FAQs on Decimals and Fractions
How to Read Decimals?
Read the whole number part followed by "and", then read the fractional part in the same way as we read whole numbers but followed by the place value of the last digit. The decimal number is always read as individual digits. As an example, we would read a decimal number of 145.367 as one hundred and forty-five point three six seven.
Are Decimals Integers?
Every Integer can be represented in the form of Decimals, for example, 12.00. But decimals are not integers as integers are not in the form of p/q. By default, an integer can be considered as a decimal. For performing arithmetic operations involving integers and decimals, the integers are to be converted as fractions. For the addition of 4 to 3.36, we convert the 4 as 4.00.
How to Turn Decimals Into Fractions?
To convert a decimal to a fraction, we follow three basic steps mentioned below:
- Rewrite the number by ignoring the decimal point.
- Divide the number by the place value of the last digit in the fractional part of the number.
- Simplify the fraction.
How to Round Decimals?
To round a decimal number look at the next digit to the right side of the place upto which we want to round off. If the digit is less than 5, round down to the previous number and if the digit is 5 or more than 5, round up to the next higher number. The decimal 3.284 can be rounded to 3.28, and a decimal of 4.68 is rounder
What Are Repeating and Non-Repeating Decimals?
Repeating Decimals are those in which one or more digits repeat again and again, for example 1/3 = 0.3333333, while non-repeating decimals are those that end after a specific number of digits, for example, 1/2= 0.5. Another example of nonrounding decimal is 22/7 = 3.142857
What Is the Relation Between Decimal and Percentage?
Every Decimal number can be expressed in the form of a percentage. We need to convert decimals to percentages when we compare two or more numbers. Both decimals and percentages are just two ways to represent a number. A decimal number can be multiplied by 100 and a percentage symbol(%) can be placed to obtain the percentage value. Also, a percentage can be divided by 100, and a percentage symbol be removed to obtain a decimal value.
What is 1/4 in Decimals?
Let us see how to represent 1/4 in decimals. Here multiply the numerator and the denominator with a 25, to obtain a 100 in the denominator. Further, we need to convert this fraction with a denominator of 100, as a decimal.
1/4 x 25/25 = 25/100 = 0.25