Percentage
The term "percentage" was adapted from the Latin word "per centum", which means "by the hundred". Percentages are fractions with 100 as the denominator. In other words, it is the relation between part and whole where the value of "whole" is always taken as 100.
For example, if the marks of a student in math are 15 out of 50 then the corresponding percentage can be calculated by expressing "marks obtained" as a fraction of "total marks" and multiplying the result by 100. i.e., percentage of marks = 15 / 50 × 100 = 30%. Learn more about percentages and how to convert them into fractions and decimals.
| 1. | What is Percentage? |
| 2. | Calculating Percentage |
| 3. | Percentage Formula |
| 4. | Conversion Between Percentages and Decimals |
| 5. | Percentage Change Between Two Numbers |
| 6. | FAQs on Percentage |
What is the Percentage?
The percentage is a fraction or a ratio in which the value of the whole (denominator) is always 100. For example, if Sam scored 30% marks in his math test, it means that he scored 30 marks out of 100. It is written as 30/100 in the fraction form and 30:100 in terms of ratio. Here "%" is the symbol of percentage and is read as "percent" or "percentage". This percent symbol can always be replaced with "divided by 100" to convert it into a fraction or decimal equivalent.
Examples of Percentage
- 10% = 10/100 ( = 1/10 (or) 0.1)
- 25% = 25/100 ( = 1/4 (or) 0.25)
- 12.5% = 12.5/100 ( = 1/8 (or) 0.125)
- 50% = 50/100 ( = 1/2 (or) 0.5)
Calculating Percentage
Calculating percentage means finding the share out of the whole, in terms of 100. There are two ways to calculate percentage:
- By changing the denominator of the fraction to 100: In this method, we just find the equivalent fraction of a given fraction such that the resultant denominator is 100. Then the numerator itself is the percentage. For example:
4/25 = 4/25 × 4/4 = 16/100 = 16% - By using the unitary method: In this method, we just multiply the fraction by 100 to get the percentage. For example, the percentage that corresponds to the fraction 4/25 is:
4/25 × 100 = 400/25 = 16%
It should be noted that the first method for calculating the percentage is not suggested in situations where the denominator is not a factor of 100. In such cases, we use the unitary method. Let's see how to find the percentage using the two methods given above in detail.
Finding Percentage When the Total is 100
When we have two or more values that add up to 100, the percentage of those individual values to the total value is that number itself. For example, Sally bought tiles of three different colors for her house. The details of the purchase are given in the following table.
| Colour | Number of Tiles | Rate per Hundred | Fraction | Percentage | Read as |
|---|---|---|---|---|---|
| Yellow | 39 | 39 | 39/100 | 39% | 39 percent |
| Green | 26 | 26 | 26/100 | 26% | 26 percent |
| Red | 35 | 35 | 35/100 | 35% | 35 percent |
Finding Percentage When the Total is NOT 100
Since the total number of items adds up to 100, the percentages could be easily calculated as shown above. What if the total number of items does not add up to 100? Let us see.
For example, Emma has a bracelet that is made up 8 red beads and 12 blue beads. Here, the total number of beads is 8 + 12 = 20 (which is not equal to 100). In this case, the percentages can be calculated as shown in the table below (using the unitary method).
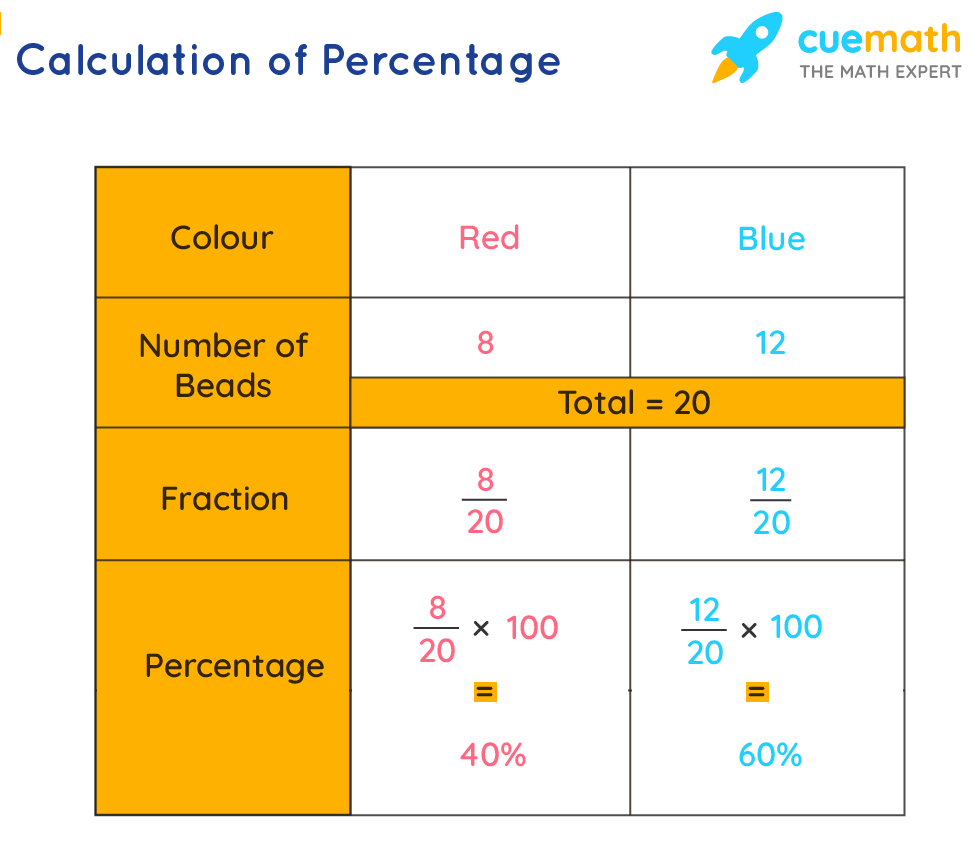
But here, the percentages can be calculated by making the denominators 100 as well. Then we get
- Percentage of red beads = 8/20 × 5/5 = 40/100 = 40%
- Percentage of blue beads = 12/20 × 5/5 = 60/100 = 60%
Look at the following example which shows the advantage of the unitary method over the other method.
Example: How to calculate the percentage of marks of a student who scored 35 out of 40 in math?
Solution: Here, the marks of the student are 35/40. But here, the denominator is not a factor of 100. Thus, finding the percentage in the unitary method is helpful here.
Percentage of marks = 35/40 × 100 = 87.5%.
Percentage Formula
The percentage formula is used to find the share of a whole in terms of 100. Using this formula, you can represent a number as a fraction of 100. If you observe carefully, all three ways to get the percentage shown above can be easily calculated by using the formula given below:
Percentage = (Value/Total Value)×100
Example: In a class of 40 children, 10 are girls. Then what is the percentage of girls?
Solution: Here, the number of girls = 10.
The total number of children = 40.
By the percentage formula,
the percentage of girls = 10/40 × 100 = 25%.
Conversion Between Percentages and Decimals
As we have already seen, the % symbol can always be replaced with "/100". The following points should be taken care of while converting percentages into decimals and vice versa.
- to convert percentages into decimals, just replace % with "divided by 100". For example, 40% = 40/100 = 0.4.
- to convert decimals into percentages, just multiply by 100. For example, 0.4 = 0.4 × 100 = 40%.
Percentage Change Between Two Numbers
Percentage change is the change in the value of a quantity over a period of time in terms of percentage. For example, an increase in population, a decrease in poverty, and so on. We have the formula to show the change in quantity as a percentage. There are two cases that might arise while calculating percentage change and those are:
- Calculate percentage increase
- Calculate percentage decrease
Percentage Increase
Percentage increase refers to the percentage change in the value when it is increased over a period of time. For example, population increase, increase in the number of bacteria on a surface, etc. Percentage increase can be calculated by using the following formula:
Percentage Increase = (Increased Value-Original value)/Original value × 100
Example: The cost of a jacket is increased from $100 to $150. Then by what percentage the price is increased?
Solution: Percentage increase = (150 - 100) / 100 × 100 = 50%.
Percentage Decrease
Percentage decrease refers to the percentage change in the value when it is decreased over a period of time. For example, decrease in the level of rainfall, decrease in the number of Covid patients, etc. Percentage decrease can be calculated by using the following formula:
Percentage Decrease= (Original value-Decreased Value)/Original Value × 100
Example: The amount of rainfall has decreased from 127 mm to 103 mm. Then what is the corresponding percentage decrease?
Solution: Percentage decrease = (127 - 103) / 127 × 100 = 18.9% (Approximately).
Important Points on Percentages:
- To calculate the percentage of a number out of the total number, just use the formula number / total number × 100.
- An increase or decrease in any quantity can be expressed as a percentage. This is referred to as percentage change.
- Fractions can be converted into percentages and vice-versa. To convert the fractions into percentages, multiply by 100. To convert percentages into fractions, divide by 100.
- Percentages are reversible. For example, 50% of 60 is the same as 60% of 50.
☛ Related Topics:
- Percentage Calculator
- Percent to Decimal Calculator
- Decimal to Percent Calculator
- Percent to Fraction Calculator
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Solved Examples on Percentage
-
Example 1: Robert got a 5% hike in his salary. His current salary is $70,000. Calculate his revised salary after promotion.
Solution:
Robert's current salary = $70,000
Hike = 5% of 70,000= 5/100 × 70,000
5 × 700 = $3500Robert's pay hike is $3500.
Thus, his new salary will be $70,000 + $3500 = $73,500.
Answer: Robert's salary after his promotion is $73,500.
-
Example 2: Neil bought a new cell phone for $90. The value of the phone decreases by 3% from its original price every year. Calculate the value of his mobile after 1 year.
Solution:
3% of 90 = 3/100 × 90 = $2.7
Thus, the value of the mobile after 1 year will be: 90 - 2.7 = $87.3
Answer: The value of the mobile after 3 years will be $87.3
-
Example 3: John spends 120 minutes in studying daily. He spends, 60 min on math, 30 min on science, and 30 min on social studies. Then find the percentage of time for each subject.
Solution:
Percentage of time for math = 60/120 × 100 = 50%
Percentage of time for science = 30/120 × 100 = 25%
Percentage of time for social studies = 30/120 × 100 = 25%
Answer: Percentages of math, science, and social studies are 50%, 25%, and 25% respectively.

Practice Questions on Percentage
FAQs on Percentage
What is the Definition of Percentage?
The percentage is defined as a given part or amount in every hundred. It is a fraction with 100 as the denominator and is represented by the symbol "%".
What are Real Life Examples of Percentages?
Some real-life examples of percentages are listed below:
- Composition of oxygen, carbon dioxide, nitrogen, etc in air.
- Your phone's or laptop's battery percentage.
- Percentage of your marks in a test.
- Percentage of nutrients on a food packet.
- Comparison of number of patients recovered from Covid between two or more cities is done in percentage etc.
How to Calculate the Average Percentage?
Here are the steps to calculate the average of the given percentages.
- Convert the percentage into decimal numbers. For example, to calculate the average of 30% of 50 and 20% of 80, we convert them into their decimal forms which are 0.3 and 0.2 respectively.
- Write the number represented by each decimal number. In this case, it will be 0.3×50=15 and 0.2×80=16 respectively.
- Add the numbers thus obtained. (15+16=31).
- Find the sum of sample sizes. (50+80=130).
- Divide the total number obtained in Step 3 by the number obtained in Step 4. So, 31/130=0.24. This decimal number represents 24% which is the required average percentage.
How Do you Minus a Percentage?
To subtract some percentage from a number, just multiply that number by the percentage you want to retain. For example, to subtract 10% out of 500, just multiply 90% by 500
How Do We Find Percentage?
The percentage can be found by dividing the value by the total value and then multiplying the result by 100. The formula used to calculate the percentage is: (value/total value)×100%.
Can Percent be More Than 100?
Yes, the percentage can be more than 100 when we have a value that is larger than the total value.
How to Find the Percentage of a Number?
The percentage of a number is the value of the number out of 100. It is calculated by using the formula (part/whole) × 100. For example, in a class, there are 26 boys and 24 girls. So, the percentage of boys in the class is 26/(26+24) × 100 = 26/50 × 100 = 52%, which means out of 100, 52 are boys.
What is Percentage Change?
Percentage change is the change in percentage from the old value to the new value. It is calculated using the following formula: Percentage change= (difference between old and new values/old value)×100%.
How to Calculate the Percentage of Marks?
To calculate the percentage of marks, just divide the marks obtained by the total marks and multiply the fraction by 100. For example, if the marks obtained are 525 and the total marks are 600, then the corresponding percentage is 525/600 ×100 = 87.5
What is the Formula for Percentages into Decimals and Vice Versa?
To convert percent to decimal, drop the percent symbol (%), divide it by 100, and write the decimal form of the fraction thus obtained. Further, to convert decimals into percentages, just multiply them by 100.
visual curriculum