Tangent Formulas

The tangent formulas are formulas about the tangent function in trigonometry. The tangent function (which is usually referred to as "tan") is one of the 6 trigonometric functions which is the ratio of the opposite side to the adjacent side. There are multiple formulas related to tangent function which can be derived from various trigonometric identities and formulas. Let us learn the tangent formulas along with a few solved examples.

What Are Tangent Formulas?

The tangent formulas talk about the tangent (tan) function. Let us consider a right-angled triangle with one of its acute angles to be x. Then the tangent formula is, tan x = (opposite side) / (adjacent side), where "opposite side" is the side opposite to the angle x, and "adjacent side" is the side that is adjacent to the angle x. Apart from this general formula, there are so many other formulas in trigonometry that will define a tangent function which you can see in the following image.

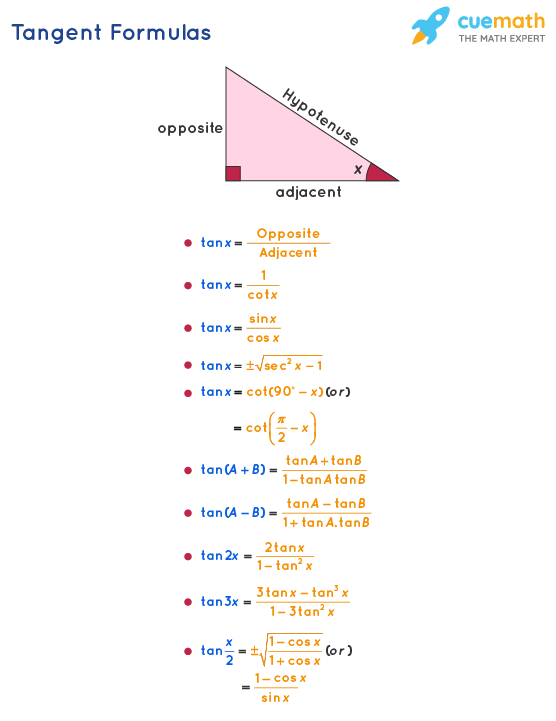
Tangent Formulas Using Reciprocal Identity

We know that the tangent function (tan) and the cotangent function (cot) are reciprocals of each other. i.e., if tan x = a / b, then cot x = b / a. Thus, tangent formula using one of the reciprocal identities is,

tan x = 1 / (cot x)

Tangent Formula Using Sin and Cos

We know that sin x = (opposite) / (hypotenuse), cos x = (adjacent) / (hypotenuse), and tan x = (opposite) / (adjacent). Now we will divide sin x by cos x.

(sin x) / (cos x) = [ (opposite) / (hypotenuse) ] / [ (adjacent) / (hypotenuse) ] = (opposite) / (adjacent) = tan x

Thus, the tangent formula in terms of sine and cosine is, 

tan x = (sin x) / (cos x)

Tangent Formulas Using Pythagorean Identity

One of the Pythagorean identities talks about the relationship between sec and tan. It says, sec²x - tan²x = 1, for any x. We can solve this for tan x. Let us see how.

sec²x - tan²x = 1

Subtracting sec²x from both sides,

-tan²x = 1 - sec²x

Multiplying both sides by -1,

tan²x = sec²x - 1

Taking square root on both sides,

tan x = ± √( sec²x - 1)

Tangent Formula Using Cofunction Identities

The cofunction identities define the relation between the cofunctions which are sin, cos; sec, csc; and tan, cot. Using one of the cofunction identities,

• tan x = cot (90^o - x) (OR)
• tan x = cot (π/2 - x)

Tangent Formulas Using Sum/Difference Formulas

We have sum/difference formulas for every trigonometric function that deal with the sum of angles (A + B) and the difference of angles (A - B). The sum/difference formulas of tangent function are,

• tan (A + B) = (tan A + tan B) / (1 - tan A tan B)
• tan (A - B) = (tan A - tan B) / (1 + tan A tan B)

Tangent Formula of Double Angle

We have double angle formulas in trigonometry which deal with 2 times the angle. The double angle formula of tan is 

tan 2x = (2 tan x) / (1 - tan²x)

Tangent Formula of Triple Angle

We have triple angle formulas for all trigonometric functions. Among them, the triple angle formula of the tangent function is,

tan 3x = (3 tan x - tan³x) / (1 - 3 tan²x)

Tangent Formula of Half Angle

We have half-angle formulas in trigonometry that deal with half of the angles (x/2). The half-angle formulas of tangent function are,

• tan (x/2) =± √[ (1 - cos x) / (1 + cos x) ]
• tan (x/2) = (1 - cos x) / ( sin x)

Examples Using Tangent Formulas

Example 1: If sec x = 5/3 and x is in the first quadrant, find the value of tan x.

Solution:

Using one of the tangent formulas,

tan x = ± √(sec²x - 1)

Since x is in the first quadrant, cos x is positive. Thus,

tan x = ± √(sec²x - 1)

Substitute sec x = 5/3 here,

tan x = √((5/3)² - 1) 

= √((25/9) - 1)

=√ (16/9)

= 4/3

Answer: tan x = 4/3.

Example 2: If cot (90 - A) = 3/2, then find the value of tan A.

Solution:

Using one of the tangent formulas,

tan A = cot (90 - A)

It is given that cot (90 - A) = 3/2. Hence,

tan A = 3/2

Answer: tan A = 3/2.

Example 3: If tan A = 1/2 and tan B = 1/3, find tan (A + B).

Solution:

Using the tangent formula of addition,

tan (A + B) = (tan A + tan B) / (1 - tan A tan B)

= (1/2 + 1/3) / ( 1 - (1/2) · (1/3) )

= (5/6) / (1 - (1/6))

= (5/6) / (5/6)

= 1

Answer: tan (A + B) = 1.