Vertex Formula
The Vertex formula of a parabola is used to find the coordinates of the point where the parabola crosses its axis of symmetry. The vertex is the point (h,k). As we know the standard equation of a parabola is y = ax2+bx+c. If the coefficient x2 is positive then the vertex is the bottom of the U- shaped curve and if it is negative the vertex point is the top of the U-shaped curve. The vertex at which the parabola is minimum (when the parabola opens up) or maximum (when the parabola opens down) and the parabola turns (or) changes its direction. Let's learn more about the vertex formula and solve examples.
What is Vertex Formula?
The vertex formula helps to find the vertex coordinates of a parabola. The standard form of a parabola is y = ax2 + bx + c. The vertex form of the parabola y = a(x - h)2 + k. There are two ways in which we can determine the vertex(h, k). They are:
- (h, k) = (-b/2a, -D/4a), where D(discriminant) = b2 - 4ac
- (h,k), where h = -b / 2a and evaluate y at h to find k.
Vertex Formula
The two vertex formulas to find the vertex is:
Formula 1: (h, k) = (-b/2a, -D/4a)
where,
- D is the denominator
- h,k are the coordinates of the vertex
Formula 2: x-coordinate of the vertex = -b / 2a
Derivation of Vertex Formulas
Formula 1
We know that the standard form of a parabola is, y = ax2 + bx + c. Let us convert it to the vertex form y = a(x - h)2 + k by completing the squares.
Subtracting c from both sides:
y - c = ax2 + bx
Taking "a" as the common factor:
y - c = a (x2 + b/a x)
Here, half the coefficient of x is b/2a and its square is b2/4a2. Adding and subtracting this on the right side (inside the parentheses):
y - c = a (x2 + b/a x + b2/4a2 - b2/4a2)
We can write x2 + b/a x + b2/4a2 as (x + b/2a)2. Thus, the above equation becomes:
y - c = a ( (x + b/2a)2 - b2/4a2)
Distributing "a" on the right side and adding "c" on both sides:
y = a (x + b/2a)2 - b2/4a + c
y = a (x + b/2a)2 - (b2 - 4ac) / (4a)
Comparing this with y = a (x - h)2 + k, we get:
h = -b/2a
k = -(b2 - 4ac) / (4a)
We know that b2 - 4ac is the discriminant (D).
Thus, the vertex formula is: (h, k) = (-b/2a, -D/4a) where D = b2 - 4ac
Formula 2
If you feel difficult to memorize the above formula, you can just remember the formula for the x-coordinate of vertex and then just substitute it in the given equation y = ax2 + bx + c to get the y-coordinate of the vertex.
x-coordinate of the vertex(h) = -b / 2a
Alternatively, if you do not want to use any of the above formulas to find the vertex, then you can just complete the square to convert y = ax2 + bx + c of the form y = a(x - h)2 + k manually and find the vertex (h, k).
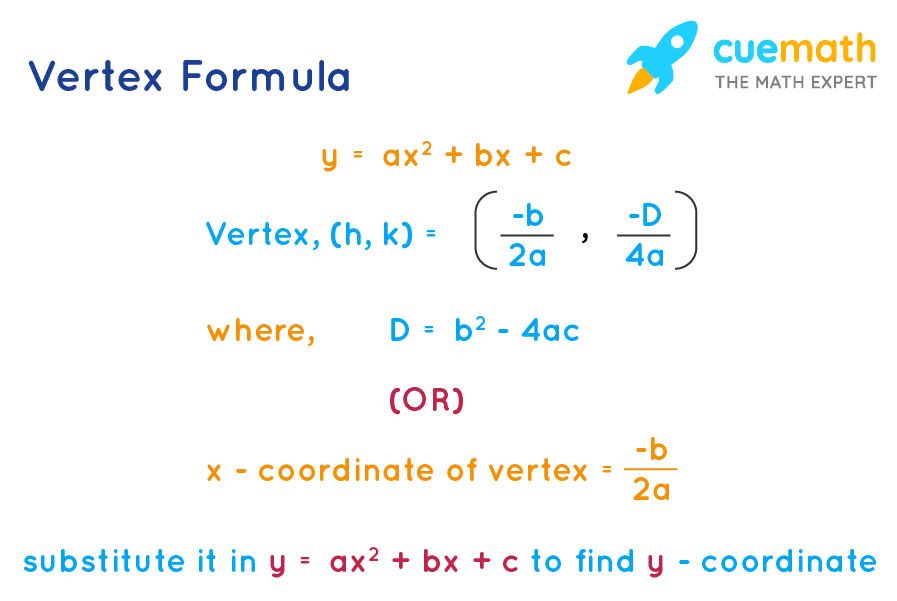

Examples Using Vertex Formula
-
Example 1: Find the vertex of y = 3x2 - 6x + 1.
Solution:
To find: The vertex of the given equation (parabola).
Comparing the given equation with y = ax2 + bx + c, we get
a = 3, b = -6, c = 1.
Then the discriminant is, D = b2 - 4ac = (-6)2 - 4(3)(1) = 36 - 12 = 24.
Using the vertex formula (formula 1),
Vertex, (h, k) = (-b/2a, -D/4a)
(h, k) =( -(-6) / (2×3), -24 / (4×3) ) = (6/6, -24/12) = (1, -2)
Therefore, The vertex of the given parabola = (1, -2).
-
Example 2: Find the vertex of a parabola whose x-intercepts are (2, 0) and (3, 0) and whose y-intercept is (0, 6).
Solution:
To find: The vertex of the parabola.
Since (2, 0) and (3, 0) are the x-intercepts of the given parabola, (x - 2) and (x - 3) are the factors of the equation of the parabola. So the equation of the parabola is of the form:
y = a (x - 2) (x - 3) .... (1)
Its y-intercept is given to be (0, 6). Substitute x = 0 and y = 6 in the above equation:
6 = a (0 - 2) (0 - 3)
6 = 6a
a = 1
Substitute a = 1 in (1):
y = 1 (x - 2) (x - 3) = x2 - 5x + 6 ... (2)
Comparing the above equation with y = ax2 + bx + c, we get
a = 1; b = -5; c = 6
Using the vertex formula (formula 2),
x-coordinate of the vertex = -b / 2a = -(-5) / (2×1) = 5/2
Substitute this in (2) to find the y-coordinate of the vertex.
y = (5/2)2 - 5 (5/2) + 6 = -1/4
Therefore, The vertex of the given parabola = (5/2, -1/4)
-
Example 3: Determine the coordinates of the vertex for the given parabola equation: y= 4x2 + 16x -16
Solution:
Given equation: y= 4x2 + 16x -16
Here a = 4, b = 16
We know that the formula to find the x- coordinate is given by -b/2a
= -16/2(4)
= -2
Therefore, x -coordinate is -2
Now, substitute the value of x in the given equation, we get
y = 4(-2)2 +16(-2) -16
y= -32
Hence, the vertex coordinates (h, k) is (-2, -32)
FAQs on Vertex Formula
What is Vertex Formula?
The Vertex formula of a parabola is used to find the coordinates of the point where the parabola crosses its axis of symmetry. The coordinates are given as (h,k). The vertex of a parabola is a point at which the parabola is minimum (when the parabola opens up) or maximum (when the parabola opens down) and the parabola turns (or) changes its direction.
What is the Formula to Find the Vertex on X Coordinates?
Using the standard form of a parabola y = ax2 + bx + c and the vertex equation y = a(x - h)2 + k, we can derive at the first formula of vertex i.e.
The vertex formula is: (h, k) = (-b/2a, -D/4a) where D = b2 - 4ac
How do you Use Vertex Formula?
Vertex formula can be used to find the vertex of any parabola using the parabola equation. The vertex formula for parabola equation y = ax2 + bx + c is given as, (h, k) = (-b/2a, -D/4a) where D = b2 - 4ac
What is the Formula to Find the Vertex on Y Coordinates?
To find the vertex (h, k), get h(x-coordinate of the vertex) = -b/2a from the standard equation y = ax2 + bx + c and then find y at h to get k (the y-coordinate of the vertex).
What is the Alternative Formula used to Find the Vertex?
The vertex formula to find the vertex coordinates (h,k)= (-b/2a, -D/4a) from the standard equation y = ax2 + bx + c, where D = b2 - 4ac.
visual curriculum