Quadratic Inequalities
Quadratic inequalities can be derived from quadratic equations. The word “quadratic” comes from the word “quadrature”, which means "square" in Latin. From this, we can define quadratic inequalities as second-degree inequation. Here, we first define a quadratic equation. The general form of a quadratic equation is ax2 + bx + c = 0. Further if the quadratic polynomial ax2 + bx + c is not equal to zero, then they are either ax2 + bx + c > 0, or ax2 + bx + c < 0, and are referred as quadratic inequalities.
In this mini-lesson, we will learn about quadratic inequality, solving quadratic inequalities, quadratic inequalities in one variable, quadratic inequalities formula, and the graph of quadratic inequality, with the help of examples, FAQs.
What Do You Mean By Quadratic Inequalities?
The quadratic inequality is a second-degree expression in x and has a greater than (>) or lesser than (<) inequality. the quadratic inequality has been derived from the quadratic equation ax2 + bx + c = 0. Let us check the definition of quadratic inequality, the standard form, and the examples of quadratic inequalities.
Definition
If a quadratic polynomial in one variable is less than or greater than some number or any other polynomial (with a degree less than or equal to 2), then it is said to be a quadratic inequality. The difference between a quadratic equation and a quadratic inequality is that the quadratic equation is equal to some number while quadratic inequality is either less than or greater than some number. Some examples of quadratic inequalities in one variable are:
- x2 + x - 1 > 0
- 2x2 - 5x - 2 > 0
- x2 + 2x - 1 < 0
Standard Form
The standard form of quadratic inequalities in one variable is almost the same as the standard form of a quadratic equation. The only difference is that the quadratic equation has an "equal to" sign in it while a quadratic inequality has a "greater than" or "less than" sign (> or <). The standard form of quadratic inequality can be represented as:
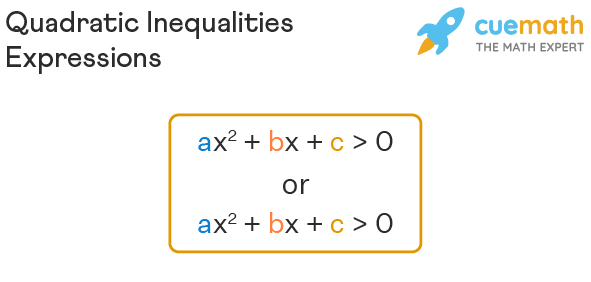
Example of Quadratic Inequality
Now, consider the scenario where you want to build a rectangular house with a length equal to two units more than twice its breadth. If you don't want the floor area of the house to be more than 1500 ft2, what length and breadth can you consider?
You know that the area of a rectangle is length times its breadth. Hence, the area of the house is (2 + 2x)x = 2x2 + 2x, where x is the breadth of the rectangular house. Now, we know that the area cannot exceed 1500 ft2. Thus, the quadratic inequality for the above scenario is as follows.
2x2 + 2x < 1500
How To Solve Quadratic Inequalities?
Solving a quadratic inequality means to find the values of x which satisfy the given condition of the question. A quadratic second degree equation ax2 + bx + c = 0 can have maximum 2 values of x. But a quadratic inequality can have more than 2 values. It can have infinite values of x which satisfy the condition ax2 + bx + c < 0 or ax2 + bx + c > 0. Solving a quadratic inequation means finding the range of values of x.
Now consider a quadratic expression ax2 + bx + c. We can write the quadratic expression in the form of (x - α)(x - β) and α < β. Using the number line method the solution for the quadratic inequality can be expressed as follows.

It means that if ax2 + bx + c > 0, then x can take values between - ∞ to α and β to +∞.
If x2 + bx + c > 0, then x ∈ (-∞ , α) U (β, + ∞)
If x2 + bx + c < 0, then x can take values between α and β.
If x2 + bx + c < 0, then x ∈ (α, β)
Let's take a quadratic inequality x2 - 1 > 0. Here the expression x2 - 1 > 0 can be factorized as (x - 1)(x + 1) > 0. This gives the values of α = -1 and β = 1. Hence, we obtain the range of x as x ∈ (-∞ , -1) U (1, + ∞)

If the quadratic inequality is x2 - 1 < 0. The expression x2 - 1 < 0, can be factorized as (x - 1)(x + 1) < 0. This gives α = -1 and β = 1. Therefore, the range of x is x ∈ (-1, 1)

If the quadratic inequality is x2 - 1 > 0 (where it shows the quadratic inequality is greater than or equal to zero). The expression x2 - 1 > 0 can be factorized as (x - 1)(x + 1) > 0. Here we obtain α = -1 and β = 1, and the range of x is x ∈ {-∞ , -1] U [+1, + ∞}

If the quadratic inequality is x2 - 1 < 0 (where it shows the quadratic inequality is less than or equal to zero). The expression x2 - 1 < 0 is factorized as (x - 1)(x + 1) < 0. Here the roots of the expression are α = -1 and β = 1, and the range of x is x ∈ [-1, +1]

Notations Used In Quadratic Inequalities
The notation of greater than (>) and lesser. than (< ) is often used in quadratic equations. The quadratic equation ax2 + bx + c = 0 is written as a quadratic equation by replacing equals to the symbol (=) with greater than or lesser than inequality. The general format of a quadratic inequality is ax2 + bx + c > 0, or ax2 + bx + c < 0. Further, let us check some of the other important notations used in quadratic inequalities.
- ( ) → Open Brackets
- [ ] → Closed Brackets
- o → Open Value( x cannot take this value)
- • → Closed Value( x can take this value)
- (-1, 1) → x cannot take value -1 and 1.
- [-1, 1) → x can take value -1 but not 1.
- (-1, 1] → x cannot take value -1 but it can take value 1.
- [-1, 1] → x can take both -1 and 1 values
☛ Related Topics
Solved Examples on Quadratic Inequalities
-
Example 1: Find the range of values of x which satisfy the quadratic inequality x2 - 7x + 10 < 0.
Solution:
First let's factorize the quadratic expression x2 - 7x + 10.
x2 - 7x + 10 < 0
x2 - 5x - 2x + 10 < 0
x(x - 5) - 2(x - 5) < 0
(x - 2)(x - 5) < 0Hence, the values of x that satisfy the quadratic inequality are x ∈ (2, 5)

Therefore we have x ∈ (2, 5).
-
Example 2: Help Mathew find the range of values of m such that the quadratic inequality x2 - mx + m > 0 is true for all values x.
Solutions:
For the quadratic expression x2 - mx + m, the coefficient of x2 is positive, and this expression is always positive and equal to zero. Hence, the discriminant of the quadratic equation is always negative and equal to zero. The discriminant of the equation is (-m)2 - 4(1)(m)
Hence we have the following inequality.
(-m)2 - 4m < 0
(-m)2 - 4m < 0
m^2 - 4m < 0
m(m - 4) < 0Thus, the values of m that satisfy the conditions for quadratic inequality are m ∈ [0, 4]

Therefore the solution of the quadratic inequality is m ∈ [0, 4].

Practice Questions on Quadratic Inequalities
FAQs on Quadratic Inequalities
How do you explain solving quadratic inequalities?
Quadratic inequalities can be solved by first factorizing the quadratic expression, then finding the range of values of x which satisfy the quadratic inequality. You can follow this section for more details on solving quadratic inequalities.
How do you solve quadratic inequalities in two variables?
An quadratic inequalities in two variables can be solved by drawing the quadratic inequalities graph of the expression. For example, the solutions of the inequality y - x2 + 1 > 0 can be solved by drawing the quadratic inequalities graph of y = x2 - 1.
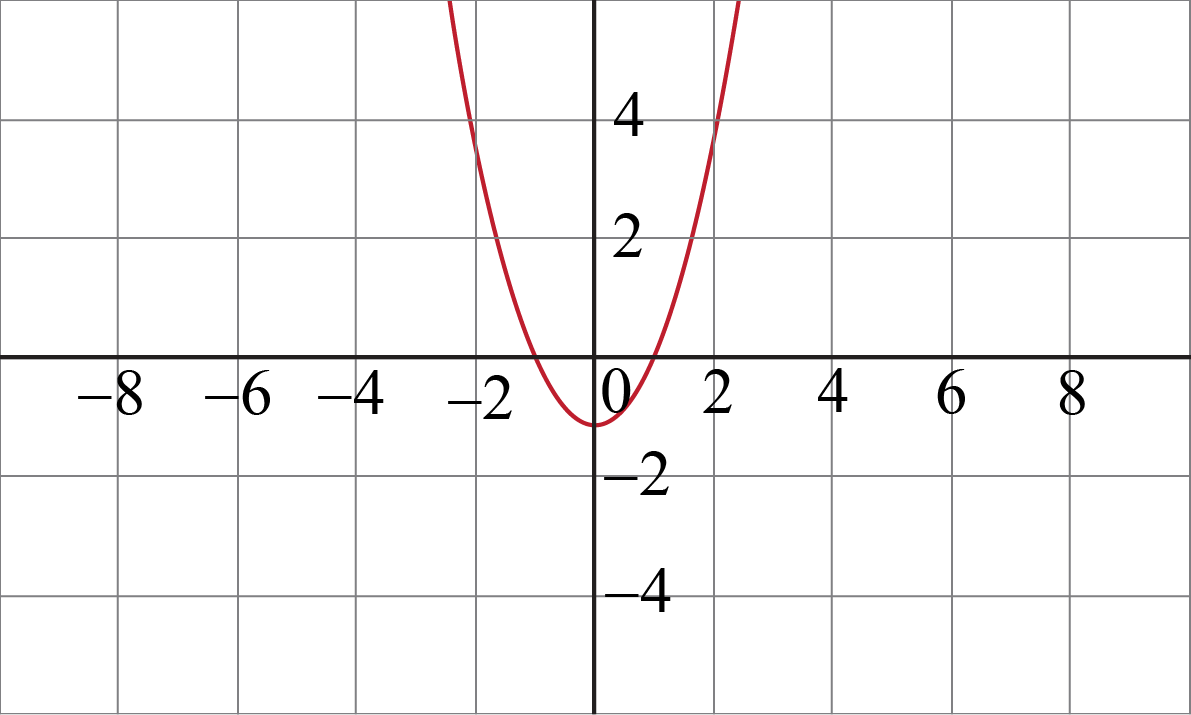
From the graph, we can clearly observe that the range of x is x ∈ (-∞, +∞) and the range of y is y ∈ (-1, +∞)
How do you solve quadratic inequalities equal to zero?
If a quadratic inequality, let's say x2 -5x - 6 > 0 is solved by equating to zero, it means that now we have to solve a quadratic equation x2 -5x - 6 = 0. The quadratic equation x2 -5x + 6 = 0 can have maximum two roots. The two values of x which satisfy the above quadratic equations are x = 2 and x = 3.
What conditions don't affect the direction of Quadratic inequality?
Adding and subtracting any number on both sides of the inequality doesn't affect the direction of the inequality. Multiplying or dividing both sides of the inequality by a negative number changes the direction of the inequality. Multiplying or dividing both sides of the inequality by a positive number doesn't affect the direction of the inequality.
How are quadratic equations solved by the factorization method?
To solve a quadratic equation with the help of the factorization method, we split the middle term (the term with x) of the equation such that when multiplying the two numbers obtained, we get the constant term. For example, the roots of the quadratic equation x2 -3x + 2 = 0 by factorization method can be obtained in the following way:
x2 - 3x + 2 = 0
x2 - 2x - x + 2 = 0
x(x - 2) -1(x - 2) = 0
(x - 1)(x - 2) = 0
Hence, x = 1 and x = 2 are the two roots of the quadratic equation.
What is the first step in solving quadratic inequality?
The first step while solving a quadratic inequality is to factorize the quadratic expression.
How do you solve quadratic inequalities word problems?
To solve a quadratic inequality word problem, first, deduce the quadratic inequality from the word problem, then solve it according to the conditions given in the question.
Can you square a quadratic inequality?
Usually, we do not prefer squaring the quadratic inequality because it might change the inequality, but for the case in which both the sides are always positive, then we can square both sides. For example, in the quadratic inequality x2 > 0, both sides of the inequality are always positive. Hence, we can square it. x4 > 0 this does not change the inequality.
How do you know if the given inequality is a quadratic inequality or not?
If the expression of the inequality is a quadratic polynomial, it will be a quadratic inequality.
What do you mean by the quadratic inequalities formula?
The quadratic inequalities formula for a quadratic equation is \(x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}\). We can factorize the quadratic expression with the help of the above quadratic formula. Then we can solve the inequality.
visual curriculum