A day full of math games & activities. Find one near you.

Direct Proportion

Direct proportion is a mathematical comparison between two numbers where the ratio of the two numbers is equal to a constant value. The proportion definition says that when two ratios are equivalent, they are in proportion. The symbol used to relate the proportions is "∝". Let us learn more about direct proportion in this article.

1.	Direct Proportion Definition
2.	Direct Proportion Formula
3.	Direct Proportion Graph
4.	Direct Proportion Vs Inverse Proportion
5.	FAQs on Direct Proportion

Direct Proportion Definition

The definition of direct proportion states that "When the relationship between two quantities is such that if we increase one, the other will also increase, and if we decrease one the other quantity will also decrease, then the two quantities are said to be in a direct proportion". For example, if there are two quantities x and y where x = number of candies and y = total money spent. If we buy more candies, we will have to pay more money, and we buy fewer candies then we will be paying less money. So, here we can say that x and y are directly proportional to each other. It is represented as x ∝ y. Direct proportion is also known as direct variation.

Some real-life examples of direct proportionality are given below:

The number of food items is directly proportional to the total money spent.
Work done is directly proportional to the number of workers.
Speed is in direct proportion to the distance w.r.t a fixed time.

Direct Proportion Formula

The direct proportion formula says if the quantity y is in direct proportion to quantity x, then we can say y = kx, for a constant k. y = kx is also the general form of the direct proportion equation.

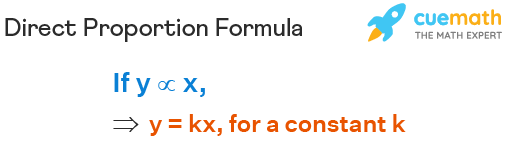
direct proportion formula

where,

k is the constant of proportionality.
y increases as x increases.
y decreases as x decreases.

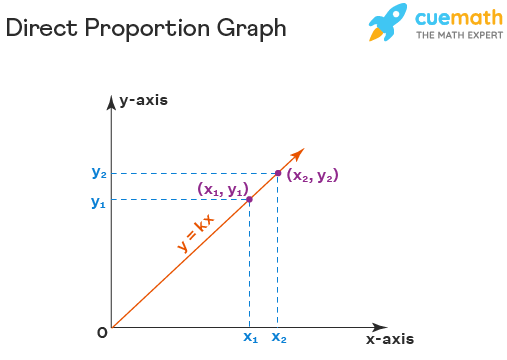
Direct Proportion Graph

The graph of direct proportion is a straight line with an upward slope. Look at the image given below. There are two points marked on the x-axis and two on the y-axis, where (x)₁ < (x)₂ and (y)₂ < (y)₂. If we increase the value of x from (x)₁ to (x)₂, we observe that the value of y is also increased from (y)₁ to (y)₂. Thus, the line y=kx represents direct proportionality graphically.

Direct proportion graph

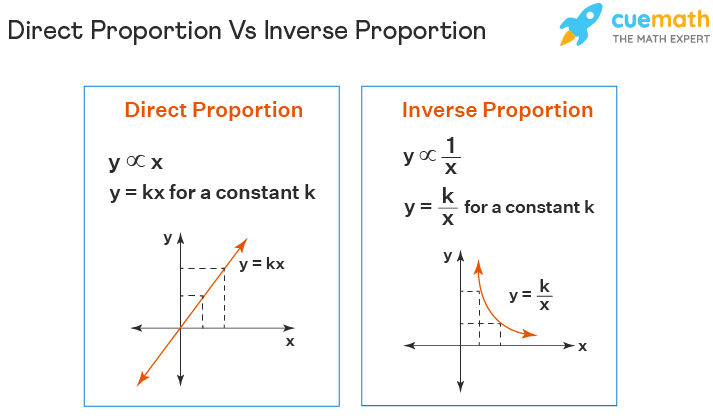
Direct Proportion Vs Inverse Proportion

There are two types of proportionality that can be established based on the relation between the two given quantities. Those are direct proportion and inverse proportional. Two quantities are directly proportional to each other when an increase or decrease in one leads to an increase or decrease in the other. While on the other hand, two quantities are said to be in inverse proportion if an increase in one quantity leads to a decrease in the other, and vice-versa. The graph of direct proportion is a straight line while the inverse proportion graph is a curve. Look at the image given below to understand the difference between direct proportion and inverse proportion.

Direct proportion vs. inverse proportion

Topics Related to Direct Proportion

Check these interesting articles related to the concept of direct proportion.

Direct Proportion Examples

Example 1: Let us assume that y varies directly with x, and y = 36 when x = 6. Using the direct proportion formula, find the value of y when x = 80?

Solution:

Using the direct proportion formula,
y = kx
Substitute the given x and y values, and solve for k.
36 = k × 6
k = 36/6 = 6
The direct proportion equation is: y = 6x
Now, substitute x = 80 and find y.
y = 6 × 80 = 480

Answer: The value of y is 480.
Example 2: If the cost of 8 pounds of apples is $10, what will be the cost of 32 pounds of apples?

Solution:

It is given that,
Weight of apples = 8 lb
Cost of 8 lb apples = $10
Let us consider the weight by x parameter and cost by y parameter.
To find the cost of 32 lb apples, we will use the direct proportion formula.
y=kx
10 = k × 8 (on substituting the values)
k = 5/4
Now putting the value of k = 5/4 when x = 32 we have,
The cost of 32 lb apples = 5/4 × 32
y =5×8
y = 40

Answer: The cost of 32 lb apples is $40.
Example 3: Henry gets $300 for 50 hours of work. How many hours has he worked if he got $258?

Solution: Let the amount received by Henry be treated as y and the number of hours he worked as x. Substitute the given x and y values in the direct proportion formula, we get,
300 = k × 50

⇒ k=300/50
k = 6
The equation is: y = 6x.
Now, substitute y = 258 and find x.
258 = 6 × x

⇒ x = 258/6 = 43 hours
Therefore, if Henry got $258, he worked for 43 hours.

go to slide go to slide go to slide

Have questions on basic mathematical concepts?

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts

Book a Free Trial Class

Direct Proportion Practice Questions

go to slide go to slide

FAQs on Direct Proportion

What is Direct Proportion in Maths?

Two quantities are said to be in direct proportion if an increase in one also leads to an increase in the other quantity, and vice-versa. For example, if a ∝ b, this implies if 'a' increases, 'b' will also increase, and if 'a' decreases, 'b' will also decrease.

What Is the Symbol ∝ Denotes in Direct Proportion Formula?

In the direct proportion formula, the proportionate symbol ∝ denotes the relationship between two quantities. It is expressed as y ∝ x, and can be written in an equation as y = kx, for a constant k.

What is Direct Proportion and Inverse Proportion?

Direct proportion, as the name suggests, indicates that an increase in one quantity will also increase the value of the other quantity and a decrease in one quantity will also decrease the value of the other quantity. While inverse proportion shows an inverse relationship between the two given quantities. It means an increase in one will decrease the value of the other quantity and vice-versa.

How do you Represent the Direct Proportional Formula?

The direct proportional formula depicts the relationship between two quantities and can be understood by the steps given below:

Identify the two quantities which vary in the given problem.
Identify the variation as the direct variation.
Direct proportion formula: y ∝ kx.

What is a Direct Proportion Equation?

The equation of direct proportionality is y = kx, where x and y are the given quantities and k is any constant value. Some examples of direct proportional equations are y = 3x, m = 10n, 10p = q, etc.

How to Solve Direct Proportion Problems?

To solve direct proportion word problems, follow the steps given below:

Identify the two quantities which vary in the given problem.
Make sure that the variation is directly proportional.
Form an equation in terms of y = kx and find the value of k base on the given values of x and y.
Find the unknown value by putting the values of x and the known variable.

How to Show Relationship Between Two Quantities Using Direct Proportion Formula?

The directly proportional relationship between two quantities can figure out using the following key points.

Identify the two quantities given in the problem.
If x/y is constant then the quantities have a directly proportional relationship.

Download FREE Study Materials

Direct Proportion Worksheets

Math worksheets and
visual curriculum