Inversely Proportional
Two quantities are said to be inversely proportional when the value of one quantity increases with respect to a decrease in another or vice-versa. This means that these two quantities behave opposite in nature. For example, the time taken to complete a task decreases with the increase in the number of workers finishing it and would increase with the decrease in the number of workers. Here, time and number of workers are inversely proportional to each other.
The other terms that can be used here for this type of proportion are inverse proportion or varying inversely or inverse variation or reciprocal proportion. Two variables say x and y, which are in inversely proportion relation are represented as x ∝ 1/y or x ∝ y-1. Directly proportional and inversely proportional are opposite relations in comparison to one another.
| 1. | What is Inversely Proportional? |
| 2. | General Formula of Inversely Proportional |
| 3. | Graphical Representation of Inverse Proportionality |
| 4. | Applications of Inversely Proportional |
| 5. | FAQs |
What is Inversely Proportional?
In Mathematics and Physics, we learn about quantities that depend upon one another, and such quantities are termed as proportional to one another. In other words, two variables or quantities are proportional to each other, if one is varied, then the other also changes by a fixed amount. This property of variables is termed proportionality and the symbol used to represent the proportionality is “∝.” There are two types of proportionality of variables. They are:
- Directly Proportional
- Inversely Proportional
When two quantities are related to each other inversely, i.e., when an increase in one quantity brings a decrease in the other and vice versa then they are said to be inversely proportional. In this, if one variable decreases, the other increases in the same proportion. It is opposite to direct proportion. Or, two quantities are said to be inversely proportional when one quantity is in direct proportion to the reciprocal of other. For example the relation between speed and time. Speed and travel time are inversely proportional because the faster we travel, the lesser is the time taken, i.e. greater the speed, the lesser the time.
- As speed increases, travel time decreases.
- And as speed decreases, travel time increases.
General Formula of Inversely Proportional
The symbol "∝" denotes the proportional relationship between two quantities. Let x and y be two quantities. Then, y being inversely proportional to x is the same thing as y being directly proportional to 1/x. It is written mathematically as y ∝ 1/x.
The general equation for inverse variation is y = k/x, where k is the constant of proportionality. We can also write this as y × x = k, or y × x = Constant. If x and y are in inverse variation and x has two values x1 and x2 corresponding to y, which also has two values y1 and y2 respectively, then by the definition of inverse variation, we have x1 y1 = x2 y2 = k.
In this case, it becomes x1 / x2 = y2 / y1 = k.
Graphical Representation of Inverse Proportionality
The nature of the graph for inversely proportional looks like this.
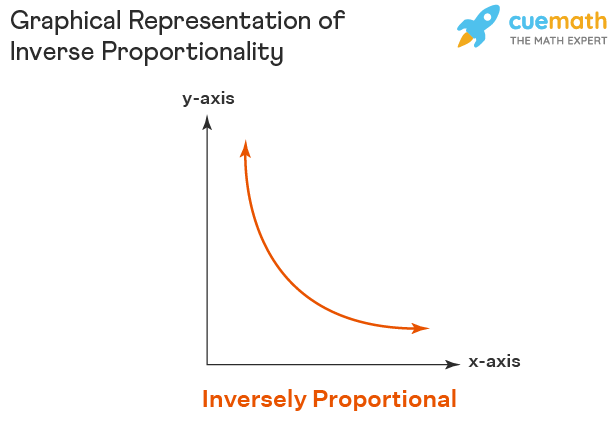
For example, the graph of the equations y = 1/x and y = -1/x having an inversely proportional relationship is shown below.

Applications of Inversely Proportional
The concept of inversely proportional is widely used in day-to-day life and also in solving many problems in the field of science, statistics, etc. There are many formulas in physics that are derived using the concept of inverse proportionality. Ohm's law, speed and time relation, the wavelength of sound, and its frequency are a few.
Important Notes on Inversely Proportional
The following points need to be remembered for inverse proportionality:
- If one quantity increases, the other decreases.
- x ∝ 1/y or y ∝ 1/x.
- x × y = k, where k is called the constant of proportionality.
Related Topics on Inversely Proportional
Check these interesting articles related to inversely proportional.
Inversely Proportional Examples
-
Example 1: A contractor appoints 36 workers to build a wall. They could finish the task in 12 days. But due to some unavoidable reasons, only 16 workers turned up. How many days will 16 workers take to finish the same task?
Solution:
There are two quantities here. Quantity 1 = Number of workers; Quantity 2 = Number of days. The information given is recorded in tabular form as shown below:
Number of workers, x 36 16 Number of days, y 12 ? Let the unknown number be "a", We use the above inversely proportional calculator table to find "a". As the number of workers reduces, the number of days required to finish the task will increase. So, there exists an inverse variation between the number of workers and the number of days. ∴ x × y = k (constant). 36 × 12 = k =16 × a, 36 × 12 = 16 × a. Thus, a = (36 × 12)/16, a = 27. Therefore, 16 workers will finish the task in 27 days.
-
Example 2: If m is inversely proportional to the square of n, and m = 64 when n = 3. Find m when n = 5.
Solution:
Given, m ∝ 1/n2. ∴ m = k/n2. m × n2 = k. From 1st condition we get, k = 64 × 32 = 576. Now, we need to find m when n = 5. m × n2 = k, m × 52 = 576. Thus, m = 576/25 = 23.04. Therefore, m = 23.04 when n = 5.

FAQs on Inversely Proportional
What does Inversely Proportional Mean?
Inversely proportional variables or quantities are those in which if one variable increases the other will decrease, and if one variable decreases the other will increase. That means when an increase in one quantity brings a decrease in the other and vice versa then they are said to be inversely proportional. For example, the time taken to do work is inversely proportional to the number of workers.
How do you know if it is Directly or Inversely Proportional?
The inversely proportional relationship between two quantities can be understood as given below,
- Identify the two quantities which vary in the given problem.
- If x/y is constant then it is directly proportional.
- If x × y is constant, then inversely proportional.
What is the Formula for Inversely Proportional?
The inverse relation formula helps in representing the inversely proportional relationship mathematically. The inverse variation formula is x × y = k or y = k/x, where x and y are two variables and k is the constant of proportionality.
What is the Opposite of Inversely Proportional?
The opposite of inversely proportional is directly proportional. It means when an increase in one quantity brings an increase in the other and vice versa then they are said to be directly proportional.
What does it Mean if 2 Things are Inversely Proportional?
Two quantities are said to be inversely proportional when the value of one quantity increases with respect to a decrease in another or vice-versa. This means that these two quantities behave opposite in nature. For example, the relation between speed and time. Speed and travel time are inversely proportional because the faster we travel, i.e. greater the speed, the lesser the time.
What is the Symbol of Inversely Proportional?
The symbol used to represent the proportionality is “∝.” Inverse proportionality relates to one quantity that is directly proportional to the reciprocal of the other quantity. We represent any two quantities in inverse proportion as, x ∝ 1/y or x ∝ y-1.
What is an Example of Inversely Proportional?
Inversely proportional relation occurs when one value increases and the other decreases, and vice-versa. For example, more workers on a job reduce the time taken to complete the task. Thus, they are inversely proportional.
visual curriculum