AA Criterion in Triangles

Introduction to Similarity:

If two triangles are similar it means that:

• All corresponding angle pairs are equal
• All corresponding sides are proportional 

However, in order to be sure that two triangles are similar, we do not necessarily need to have information about all sides and all angles.

What is AA similarity criterion?

The AA criterion for triangle similarity states that if the three angles of one triangle are respectively equal to the three angles of the other, then the two triangles will be similar. In short, equi-angular triangles are similar.

Ideally, the name of this criterion should then be the AAA(Angle-Angle-Angle) criterion, but we call it as AA criterion because we need only two pairs of angles to be equal - the third pair will then automatically be equal by angle sum property of triangles.

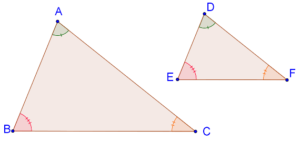
Consider the following figure, in which \(\Delta ABC\) and \(\Delta DEF\) are equi-angular,i.e.,

• \(\angle A\) = \(\angle D\) 
• \(\angle B\) = \(\angle E\) 
• \(\angle C\) = \(\angle F\)

Using the AA criterion, we can say that these triangles are similar. This means that their sides will also be proportional, that is:

\[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DF}}\]

Proof of AA similarity criterion:

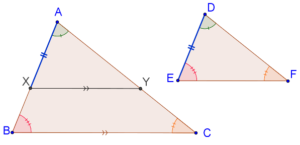
Consider the equi-angular triangles, \(\Delta ABC\) and \(\Delta DEF\)

Given: \(\angle A\) = \(\angle D\), \(\angle B\) = \(\angle E\) and \(\angle C\) = \(\angle F\).

To prove:  \(\Delta DEF\) is similar to \(\Delta ABC\)

Construction: Assume that \(AB > DE\).

• Take a point \(X\) on \(AB\) such that \(AX = DE\)
• Through \(X\), draw segment \(XY\) parallel to \(BC\) to meet \(AC\) at \(Y\)

Since \(XY\parallel BC\),

\[ \Rightarrow \Delta AXY \sim \Delta ABC....(1)\] 

Now compare \(\Delta AXY\) with \(\Delta DEF\):

1. \(\angle A\) = \(\angle D\) (given)

2. \(\angle AXY\) = \(\angle E\)  (\(XY\parallel BC\))

3.  \(AX = DE\) (by our choice of the point X)

By the ASA criterion, \(\Delta AXY\) is congruent to \(\Delta DEF\),

\[ \Rightarrow \Delta AXY \sim \Delta DEF....(2)\]

Thus from (1) and (2),

\[\boxed{\Delta DEF \sim \Delta ABC}\]

This completes our proof.

Challenge: According to the AA similarity criterion, two triangles are similar if they have at least how many corresponding angles with equal measure?