Lateral Area of a Right Triangular Prism
The lateral area of a right triangular prism is the area that is obtained by summing the areas of its side faces. In a right triangular prism, the three rectangular sides are congruent. Also, the two triangular bases at the top and the bottom are parallel and congruent to each other. The rectangular or lateral faces are perpendicular to the triangular bases. Based on our understanding of the shape of a right triangular prism, let's find out what is a lateral area of a right triangular prism.
What is Lateral Area of a Right Triangular Prism?
The lateral area of a right triangular prism is the number of unit squares that can fit into it. A right triangular prism is a polyhedron with polygons as its faces. It has 6 vertices, 5 faces, and 9 edges. Out of the 5 faces, triangles form the top and the base and rectangles form the lateral/vertical faces. The lateral area of a right triangular prism is also known as the lateral surface area of a triangular prism. The unit of the lateral area of a right triangular prism is given in square units, that is m2, cm2, in2, or ft2, etc depending upon the given units.

The 2-D net of a right triangular prism looks like a combination of 2 triangles and 3 rectangles. Therefore, 2 triangles and 3 rectangles come together to form a right triangular prism.

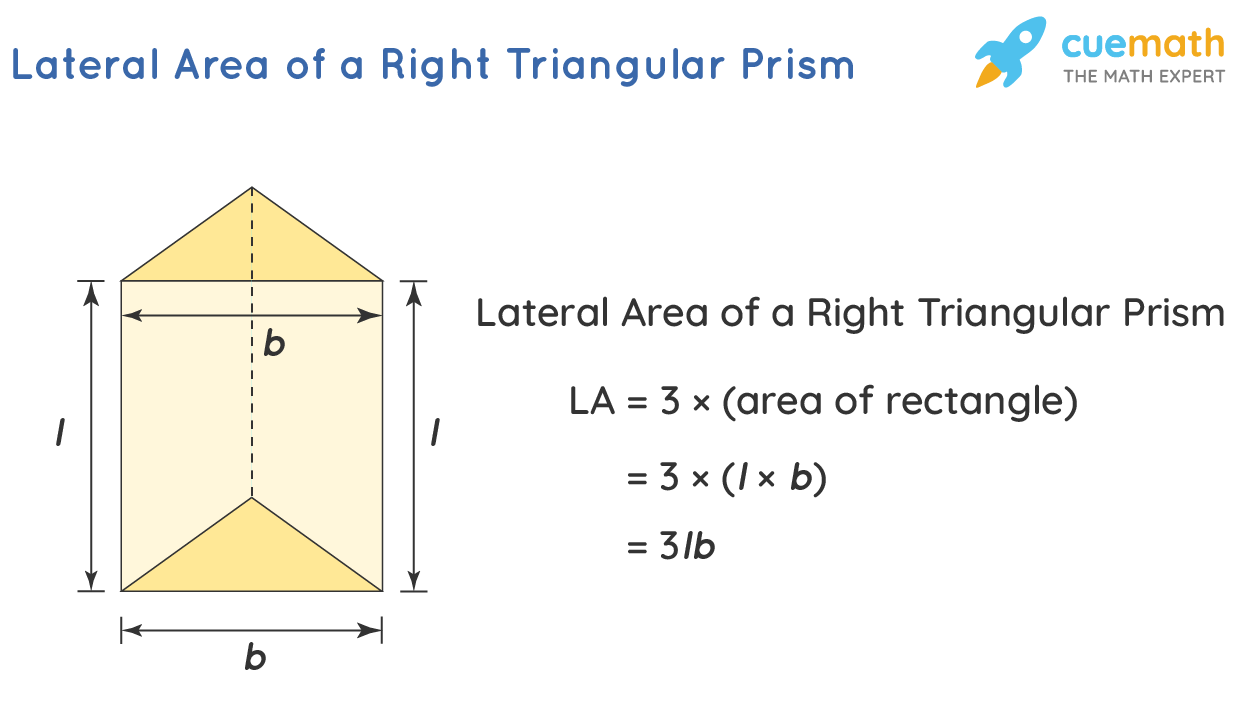
Formula of the Lateral Area of a Right Triangular Prism
The lateral area of a right triangular prism consists of the area of the vertical faces of the right triangular prism. Since rectangles form the vertical sides, therefore, to find the lateral area of a right triangular prism, we can find the area of each of the individual rectangles and then add them up.
Lateral Area of a right triangular prism, LA = Sum of areas of the vertical faces.
⇒ LA = Sum of areas of 3 rectangles.
⇒ LA = 3 × (area of a rectangle)
⇒ LA = 3 × (l × b)
⇒ LA = 3lb where, l is the length of the rectangle, and b is the breadth of the rectangle.
How to Find the Lateral Area of a Right Triangular Prism?
We can find the lateral area of a right triangular prism using the following steps:
- Step 1: Identify the length and breadth of the vertical rectangular faces.
- Step 2: Find the area of a rectangular face by multiplying the length and breadth of the rectangular faces.
- Step 3: Now multiply the obtained by 3, as there are three such faces.
- Step 4: Represent the unit in square units.
Example: Find the lateral area of a right triangular prism, whose one triangular face 6 units long and 3 units wide.
Solution: Given l = 6 units and b = 3 units
Lateral area of the right triangular prism = 3 × (l × b)
⇒ LA = 3 × (6 × 3) = 54 square units
Thus, the lateral area of the right triangular prism is 54 square units.
Examples on Lateral Area of a Right Triangular Prism
-
Example 1: Find the breadth of the rectangular face if the lateral of the right triangular prism is 105 square units and the length of a rectangular face is 7 units.
Solution: Given, LA = 105 square units and l = 7 units. Let the breadth of the rectangular face is "b".
Therefore, lateral area of the right triangular prism, LA = 3 × Area of the rectangle at the vertical face
LA = 3 × (l × b)
⇒ 105 = 3 × (7 × b)
⇒ b = 105/21 = 5 unitsTherefore, the breadth of the rectangular face is 5 units.
-
Example 2: Find the lateral area of a right triangular prism if the area of one rectangular face is 25 square units.
Solution: Given the area of one rectangular face is 25 square units.
We know the lateral area of the right triangular prism, LA = 3 × Area of the 3 rectangular faces:
⇒ LA = 3 × 25
⇒ LA = 75 square unitsTherefore, the lateral area of the right triangular prism is 75 square units.

Practice Questions on the Lateral Area of a Right Triangular Prism
FAQs on the Lateral Area of a Right Triangular Prism
What is the Lateral Area of a Right Triangular Prism?
The lateral area of a right triangular prism is defined as the number of unit squares that can be fit into a right triangular prism. A right triangular prism has three rectangular sides which are congruent. Also, the two triangular bases at the top and the bottom are parallel and congruent to each other. The rectangular or lateral faces are perpendicular to the triangular bases.
What Units Are Used for Lateral Area of a Right Triangular Prism?
The unit of 'area' is "square units". For example, it can be expressed as m2, cm2, in2, etc depending upon the given units.
What is the Formula of the Lateral Area of a Right Triangular Prism?
The formula of the lateral area of a right triangular prism is given as LA = 3lb, where l is the length of the rectangle and b is the breadth of the rectangle. The formula the lateral area of a right triangular prism shows the direct dependence of the area of a rectangular face on it.
How to Find Lateral Area of a Right Triangular Prism?
The steps to determine the lateral area of a right triangular prism are:
- Step 1: Identify the length and breadth of the rectangular faces.
- Step 2: Now determine the area of a rectangular face by multiplying the length and breadth of the rectangular faces.
- Step 3: Multiply the obtained by 3, as there are three such faces.
- Step 4: Write the obtained answer with square units.
How to Find the Length of the Rectangular Face If Lateral Area of a Right Triangular Prism Is Known?
The steps to determine the length of the rectangular face if its lateral area is known are:
- Step 1: Identify the given dimensions of the right triangular prism and let the length of the rectangular face is "l"
- Step 2: Now substitute the values in the formula, A = 3lb.
- Step 3: Solve for "l".
- Step 4: Write the obtained answer with units.
How to Find the Lateral Area of a Right Triangular Prism If Its Total Surface Area is Known?
The steps to determine find the lateral area of a right triangular prism if the total surface area is known are:
- Step 1: Identify the given dimensions for the triangular prism
- Step 2: Now subtract the areas of the triangles at the top and the bottom from the total surface area.
- Step 3: Write the obtained answer with square units.
What Happens to the Lateral Area of a Right Triangular Prism If the Length and Breadth of One Rectangular Face are Tripled?
The lateral area of the right triangular prism becomes 9 times its original value as "l" and "b" are substituted by "3l" and "3b" in the formula of the lateral area of a right triangular prism as A = 3lb = A = 3×(3l)×(3b) = 9 (3lb) which gives 9 times the original value of the lateral area.
visual curriculum