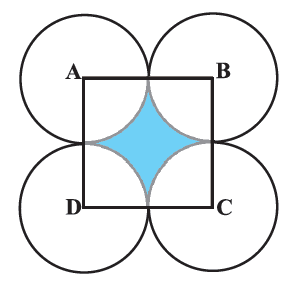
In Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region

Solution:

We use the concepts of areas of circles and squares to solve the problem.

Since the circles are touching each other externally, visually it is clear that the radius of each circle, r = 1/2 × (side of the square)

Also, ABCD being a square all angles are of measure 90°. Therefore, all sectors are equal as they have the same radii and angle.

∴ The angle of each sector (θ) = 90° [Since it is a part of a square]

∴ Area of each sector = θ/360° × πr²

= 90°/360° × πr²

= πr²/4

Area of each of the 4 sectors is equal as each sector subtends an angle of 90° at the center of a circle with radius, r = 1/2 × 14 cm = 7 cm

= 1/4 × 22/7 × 7 cm × 7 cm

= 77/2 cm²

Area of shaded region = Area of square - 4 × Area of each sector

= (14)² cm² - 4 × 77/2 cm²

= 196 cm² - 154 cm²

= 42 cm²

☛ Check: NCERT Solutions for Class 10 Maths Chapter 12

Video Solution:

In Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.3 Question 7

Summary:

The area of the shaded region of a square ABCD of side 14 cm where four circles are drawn with A, B, C, D as centers such that each circle touch externally two of the remaining three circles is 42 cm².

☛ Related Questions:

• Fig. 12.26 depicts a racing track whose left and right ends are semicircular. Fig. 12.26 The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :(i) the distance around the track along its inner edge(ii) the area of the track.
• In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
• The area of an equilateral triangle ABC is 17320.5 cm2 . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)
• On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.