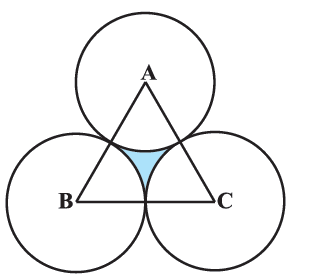
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)
Solution:
We use the formula for the area of the circle and the area of the triangle to solve the problem.
Given that, Area of equilateral ΔABC = 17320.5 cm2
√3/4 (side)2 = 17320.5 cm2
(side)2 = (17320.5 × 4)/√3 cm2
= (17320.5 × 4)/1.73205 cm2
side = √10000 × 4 cm²
= 100 × 2 cm
= 200 cm
Radius (r) = 1/2 × (length of side of triangle)
= 1/2 × 200 cm
= 100 cm
All interior angles of an equilateral traingle are of measure 60° and all 3 sectors are made using these interior angles.
∴ Angles subtended at the center by each sector (θ) = 60°
Area of each sector = θ/360° × πr2
Area of 3 sectors = 3 × 60°/360° × πr2
= 3 × 1/6 × 3.14 × (100 cm)2
= 15700 cm2
Area of shaded region = Area of ΔABC - Area of 3 sectors
= 17320.5 cm2 - 15700 cm2
= 1620.5 cm2
☛ Check: Class 10 Maths NCERT Solutions Chapter 12
Video Solution:
The area of an equilateral triangle ABC is 17320.5 cm² . With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region.
NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.3 Question 10:
Summary:
The area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle as shown in the figure. The area of the shaded region is 1620.5 cm2.
☛ Related Questions:
- On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig. 12.29). Find the area of the remaining portion of the handkerchief.
- In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the(i) quadrant OACB,(ii) shaded region
- In Fig. 12.31, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14).
- AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB = 30°, find the area of the shaded region.
visual curriculum