In quadrilateral ACBD, AC = AD and AB bisects ∠A (see Fig. 7.16). Show that Δ ABC ≅ Δ ABD. What can you say about BC and BD?

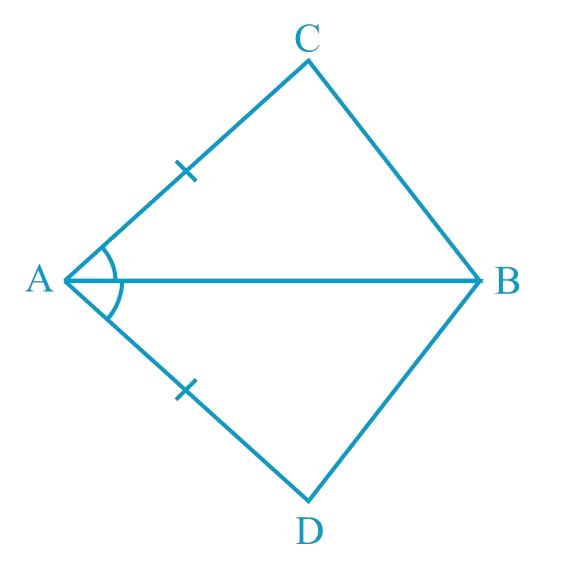
Solution:

Given: AC = AD and AB bisects ∠A

To Prove: Δ ABC ≅ Δ ABD 

We can show two sides and included angle of ABC are equal to the corresponding sides and included angle of ABD.

In Δ ABC and Δ ABD,

AC = AD (Given)

∠CAB = ∠DAB (AB bisects ∠A)

AB = AB (Common)

∴ Δ ABC ≅ Δ ABD (By SAS congruence rule)

∴ BC = BD (By CPCT)

Therefore, BC and BD are of equal lengths.

☛ Check: NCERT Solutions for Class 9 Maths Chapter 7

Video Solution:

In quadrilateral ACBD, AC = AD and AB bisects ∠A (see Fig. 7.16). Show that Δ ABC ≅ Δ ABD. What can you say about BC and BD?

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.1 Question 1

Summary:

If in quadrilateral ACBD, AC = AD, and AB bisects ∠A, we see that Δ ABC ≅ Δ ABD using SAS congruence and hence, BC and BD are of equal lengths by CPCT.

☛ Related Questions:

• ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see the given figure). Prove thati) △ ABD ≅ △ BACii) BD = ACiii) ∠ABD = ∠BAC
• AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
• l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA.
• Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:i) ΔAPB ≅ ΔAQBii) BP = BQ or B is equidistant from the arms of ∠A