In the given figures below, decide whether l is parallel to m

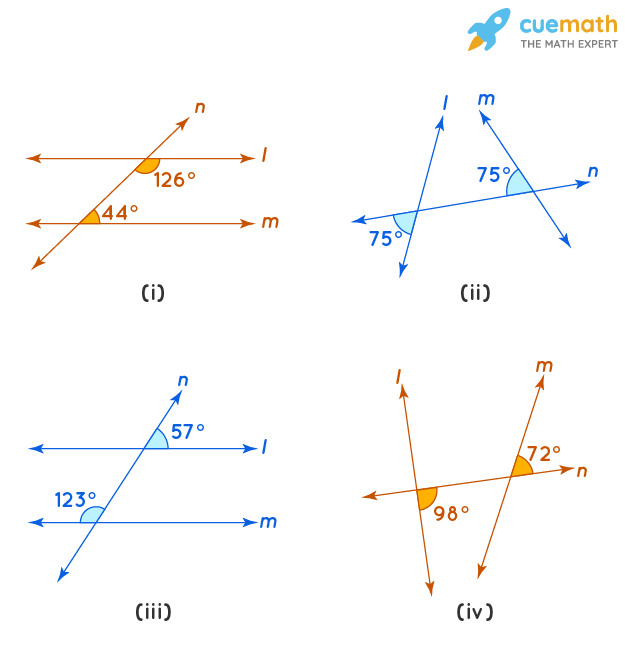
Solution:

We use the concepts of parallel lines, alternate interior angles, supplementary angles, vertically opposite angles and adjacent angles to solve the problem.

(i) Let’s visually model this problem. There is one operation that can be done, check whether interior angles are supplementary or not.

According to this model, the resulting sum of co-interior angles 126° + 44° is 170°. Now, it’s a matter of finding 𝑙 is parallel to 𝑚 or not.

Here, 126° + 44° = 170°

As the sum of co-interior angles on the same side of transversal is not 180°, therefore, l is not parallel to m.

(ii) Let’s visually model this problem. There are two operations that can be done in a sequence.

First, find the value of 𝑥 which is the angle corresponding to 75° and then check if it is equal to its corresponding angle or not.

According to this model, the resultant value of x is not equal to its corresponding angle.

Now, it’s a matter of finding 𝑙 is parallel to 𝑚 or not

∠𝑥 + 75° = 180° (Linear pair)

∠𝑥 = 180° − 75°

∠𝑥 = 105°

For l and m to be a parallel measure of their corresponding angles should be equal but here the measure of ∠𝑥 is 105° and its corresponding angle is 75°.

Therefore, the lines l and m are not parallel.

(iii) Let’s visually model this problem. There are two operations that can be done in a sequence.

First, find the value of 𝑥 which is an adjacent angle to 123° and then check it is equal to its corresponding angle or not.

∠𝑥 + 123° = 180°(Linear pair)

∠𝑥 = 180° − 123°

∠𝑥 = 57°

Here, the measure of corresponding angles are equal to 57°. Therefore, lines l and m are parallel to each other.

(iv) Let’s visually model this problem. There are two operations that can be done in a sequence.

First, find the value of x (angle adjacent to 98°) by using linear pair and then check it is equal to its corresponding angle or not. According to this model, the resultant value of x is not equal to its corresponding angle. Now, it’s a matter of finding 𝑙 is parallel to 𝑚 or not

∠𝑥 + 98° = 180° (Linear pair)

∠𝑥 = 180° − 98°

∠𝑥 = 82°

For l and m to be a parallel measure of their corresponding angles should be equal but here the measure of corresponding angles are 82° and 72° which are not equal.

Therefore, l and m are not parallel to each other.

☛ Check: NCERT Solutions for Class 7 Maths Chapter 5

---

Video Solution:

In the given figures below, decide whether l is parallel to m

NCERT Solutions for Class 7 Maths Chapter 5 Exercise 5.2 Question 6

Summary:

(i) As the sum of interior angles on the same side of transversal n is not 180°, therefore, l is not parallel to m, (ii) lines l and m are not parallel as corresponding angles are not equal, (iii) the measure of corresponding angles are equal 𝑖. 𝑒 57°. Therefore, lines l and m are parallel to each other, (iv) lines l and m are not parallel as corresponding angles are not equal.

---

☛ Related Questions:

• State The Property That Is Used In Each Of The Following Statements I If A B Then 1 5 Ii If 4 6 Then A B Iii If 4 5 180 Then A B
• In The Adjoining Figure Identify I The Pairs Of Corresponding Angles Ii The Pairs Of Alternate Interior Angles
• In The Adjoining Figure P Q Find The Unknown Angles
• Find The Value Of X In Each Of The Following Figures If L M