If segment LN is congruent to segment NP and ∠1 ≅ ∠2, prove that ∠NLO ≅ ∠NPM. Overlapping triangles LNO and PNM. The triangles intersect at point Q on segment LO of triangle LNO and segment MP of triangle PNM.
Solution:
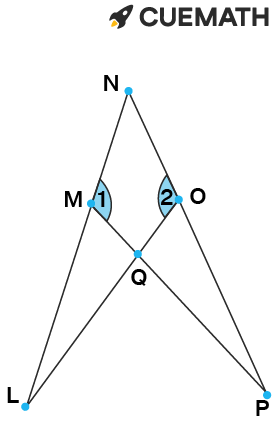
Overlapping triangles LNO and PNM.
The triangles intersect at point Q on segment LO of triangle LNO and segment MP of the triangle
By using the congruence property in triangles, we can prove ∠NLO ≅ ∠NPM
| Statements | Reasons |
|---|---|
| segment LN ≅ segment NP | Given |
| ∠ 1 ≅ ∠ 2 | Given |
| ∠ N ≅ ∠ N | Reflexive Property |
| ∠ NLO ≅ ∠ NPM | By using Angle-Angle-Side Postulate |
| ∠NLO ≅ ∠NPM | Corresponding Parts of Congruent Triangles Are Congruent(CPCTC) |
Thus ∠NLO ≅ ∠NPM using the congruence property known as Angle-Angle-Side Postulate of Hector geometry
If segment LN is congruent to segment NP and ∠1 ≅ ∠2, prove that ∠NLO ≅ ∠NPM. Overlapping triangles LNO and PNM. The triangles intersect at point Q on segment LO of triangle LNO and segment MP of triangle PNM.
Summary:
By using Angle-Angle-Side Postulate of Hector geometry it is proved that∠ NLO ≅ ∠ NPM, if segment LN is congruent to segment NP and ∠1 ≅ ∠2, Overlapping triangles LNO and PNM. The triangles intersect at point Q on segment LO of triangle LNO and segment MP of triangle PNM.