Trigonometry Ratios of Complementary Angles

Introduction:

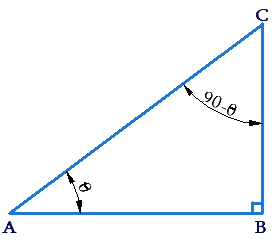
Observe the following figure:

 

Here, in \(\Delta ABC\), the sum of \(\angle A\) and \(\angle C\) is \(90^\circ \),
So, we can say that \(\angle A\) and \(\angle C\) are complementary angles.

Now, let's see the trigonometric ratios of these complementary angles.

---

Trigonometry Ratios of Complementary Angles:

Consider \(\Delta ABC\) again,

If \(\angle A = \theta \) then, \(\angle B = 90^\circ  - \theta \).

Note that \(\sin \theta = \frac{{BC}}{{AC}}\) and \(\cos\; ({90^\circ} - \theta )\) is also \(\frac{{BC}}{{AC}}\). Thus, for any angle \(\theta \),

\[\sin \theta = \cos \left( {{{90}^\circ} - \theta } \right)\]

Similarly, we observe the following relations involving complementary angles:

\[\begin{align}&\cos \theta = \sin ({90^\circ } - \theta )\; =\; \frac{{AB}}{{AC}}\\&\tan \theta = \cot ({90^\circ} - \theta ) \;=\; \frac{{BC}}{{AB}}\\&\sec \theta = \text{cosec}({90^\circ } - \theta ) = \frac{{AC}}{{AB}}\\&\text{cosec}\;\theta = \sec ({90^\circ } - \theta ) = \frac{{AC}}{{BC}}\\&\cot \theta = \tan ({90^\circ } - \theta ) = \frac{{AB}}{{BC}}\end{align}\]

We see that the following pairs of trigonometric ratios satisfy this complementary behaviour:

• sine & co-sine \(\left( {\sin {\text{& }}\cos } \right)\)
• tangent & co-tangent \(\left( {\tan {\text{& }}\cot } \right)\)
• secant & co-secant \(\left( {\sec {\text{& cosec}}} \right)\)

Note: For any of these pairs, one of the two trigonometric ratios of \(\left( {{{90}^\circ } - \theta } \right)\) will be the other trigonometric ratios of \(\theta \).

This complementary behavior of trigonometric ratios has a wide range of applications, as the following examples will show.

---

Solved Examples:

Example 1: Find the value of:

\[E = \sin {37^\circ }\cos {53^\circ } + \cos {37^\circ }\sin {53^\circ }\]

Solution: We note that,

\[\begin{align}&\sin {53^\circ } = \cos ({90^\circ } - {53^\circ }) = \cos {37^\circ }\\&\cos {53^\circ } = \sin ({90^\circ } - {53^\circ }) = \sin {37^\circ }\end{align}\]

Thus,

\[\begin{align}\boxed {E = {\sin ^2}{37^\circ } + {\cos ^2}{37^\circ } = 1}\\ \end{align}\]

This particular problem could also have been solved using the following sum identity:

\[\sin \;(A + B) = sin\;A\;cos\;B + \cos A\sin B\]

Thus,

\[E = \sin \;({37^\circ } + {53^\circ }) = \sin {90^\circ } = 1\]

Challenge 1: Find the value of:

\[E = \tan {46^\circ }\cot {44^\circ } + \cot {46^\circ }\tan {44^\circ }\]

⚡Tip: Use a similar approach as in example-1.

---

Example 2: Evaluate the value of the following expression:

\[E = \frac{{\cos {{58}^\circ }}}{{\sin {{32}^\circ }}} + \frac{{\sin {{22}^\circ }}}{{\cos {{68}^\circ }}} - \frac{{\cos {{38}^\circ }\text {cosec}{{52}^\circ }}}{{\tan {{18}^\circ  }\tan {{35}^\circ }\tan {{72}^\circ }\tan {{55}^\circ }}}\]

Solution: This expression may look complicated but is actually pretty simple to evaluate. For the first two terms, we note that

\[\begin{array}{l} \cos {58^\circ } = \sin \left( {{{90}^\circ } - {{58}^\circ }} \right) = \sin {32^\circ }\\ \sin {22^\circ } = \cos \left( {{{90}^\circ } - {{22}^\circ }} \right) = \cos {58^\circ } \end{array}\]

Thus the value of each of the first  two terms is 1.

Now, let’s come to the third term. The numerator is,

\[\begin{align}&\cos {38^\circ }{\mathop{\rm cosec}\nolimits} {52^\circ } = \frac{{\cos {{38}^\circ }}}{{\sin {{52}^\circ }}}\\&\qquad\qquad\qquad \;\;= \frac{{\cos {{38}^\circ }}}{{\cos \left( {{{90}^\circ } - {{52}^\circ }} \right)}}\\ &\qquad\qquad\qquad\;\;= \frac{{\cos {{38}^\circ }}}{{\cos {{38}^\circ }}} = 1\end{align}\]

The denominator is,

\[\begin{align}&\tan {18^\circ }\tan {35^\circ }\tan {72^\circ }\tan {55^\circ }\\& = \tan {18^\circ }\tan {35^\circ }\cot \left( {{{90}^\circ } - {{72}^\circ }} \right)\cot \left( {{{90}^\circ } - {{55}^\circ }} \right)\\ &= \tan {18^\circ }\tan {35^\circ }\cot {18^\circ }\cot {35^\circ }\\& = \left( {\tan {{18}^\circ }\cot {{18}^\circ }} \right)\left( {\tan {{35}^\circ }\cot {{35}^\circ }} \right)\\ &= 1 \times 1 = 1\end{align}\]

Thus,

\[\boxed {E = 1 + 1 - \frac{1}{1} = 1}\]

---

Example 3: Find the value of the following expression:

\[E = \tan {1^\circ }\tan {2^\circ }\tan {3^\circ }.......\tan {89^\circ }\]

Solution: \(E\)  is a product of 89 terms. If we consider the product of the first and the last term, we have:

\[\begin{align}&\tan {1^\circ }\tan {89^\circ }\; = \tan {1^\circ }\cot \left( {{{90}^\circ } - {{89}^\circ }} \right)\\&\qquad\qquad\qquad = \tan {1^\circ }\cot {1^\circ }\;\;= 1\end{align}\]

Similarly, take the product of the second and second last terms:

\[\tan {2^\circ }\tan {88^\circ } = \tan {2^\circ }\cot {2^\circ } = 1\]

Thus, we can group the terms in \(E\) into pairs, each of whose product is 1.

One term will still be left: \(\tan {45^\circ }\). But the value of this term is also 1. For this, please go through the trigonometric ratios of specific angles.

Thus,

\[\boxed {E=1}\]

Challenge 2: Find the value of the following expression:

\[E = \tan {48^\circ }\tan {23^\circ }\tan {42^\circ }\tan {67^\circ }\]

⚡Tip: Pair up complementary angles.

---

Example 4: If \(\tan 2A = \cot \left( {A - {{21}^\circ }} \right)\), where \(2A\) is an acute angle, find \(A\).

Solution: We have,

\[\begin{align}\tan 2A &= \tan \left( {{{90}^\circ } - \left( {A - {{21}^\circ }} \right)} \right)\\ \qquad\quad&= \tan \left( {{{111}^\circ } - A} \right)\\ \Rightarrow 2A &= {111^\circ } - A\end{align}\]

\[ \Rightarrow \boxed{A = 37^\circ }\]

Challenge 3: If \(\sin 3A = \cos \left( {A - 26^\circ } \right)\), where \(3A\) is an acute angle, find the value of \(A\).

⚡Tip: Use a similar approach as in example-4.

---

Example 5 : In any right \(\Delta ABC\), prove that

\[\sin \left( {\frac{{B + C}}{2}} \right) = \cos \frac{A}{2}\]

Solution: We have,

\[\begin{align}LHS=\sin \left( {\frac{{B + C}}{2}} \right) &= \sin \left( {\frac{{{{180}^\circ } - A}}{2}} \right)\\ \qquad\qquad\qquad&= \sin \left( {{{90}^\circ} - \frac{A}{2}} \right)\\ \qquad\qquad\qquad&= \cos \frac{A}{2} = RHS\end{align}\]

Hence Proved.

---