Weighted Mean
Weighted mean is a type of average that helps in contributing equally to the final mean when some data points are weighted more than the others. It is most commonly used in statistics when the data is associated with the population. If the data is weighted the same across the entire set, then the weighted mean is equal to the arithmetic mean. Let us learn more about the weighted mean, the formula, and solve a few examples to understand the concept better.
| 1. | What is Weighted Mean? |
| 2. | How to Calculate the Weighted Mean? |
| 3. | Weighted Mean Formula |
| 4. | Weighted Mean Vs Arithmetic Mean |
| 5. | FAQs on Weighted Mean |
What is Weighted Mean?
The weighted mean is a type of mean that is calculated by multiplying the weight associated with a particular event or outcome with its associated quantitative outcome and then summing all the products together. In other words, when some values weigh more than the others that's when the weighted mean is calculated.
Weighted Mean Definition
The weighted mean is defined as the summation of the product of weights and quantities, divided by the summation of weights. The concept of the weighted mean is quite often used in accounts, to give different weights based on time or based on priority.
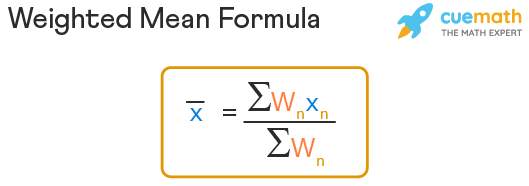
How to Calculate the Weighted Mean?
While finding the average for an equally weighted set of values, we use the simple process of the arithmetic mean. Where all the values are added and divided by the total number of items in the set. However, the weighted mean is calculated when one of the values has more weight than the others. It can be calculated by using these two simple steps:
- Multiply the numbers in the set by the weights.
- Add the results.
But in certain values, the given data set is more important than the others. A weight (w)n is attached to each of the values (x)n. The general formula to find the weighted mean is given as,
Weighted mean = Σ(w)n (x̄)n/Σ(w)n
where,
- x̄ = the mean value of the set of given data.
- w = corresponding weight for each observation.
The simple steps used to calculate the weight mean through the formula is:
- Step 1: Add all the weighted values together.
- Step 2: Multiply the weighted values and the quantities in the data set.
- Step 3: Add the values together obtained in step 2.
- Step 4: Divide the result by the number obtained in step 1.
Weighted Mean Formula
The weighted mean formula helps to find the mean of the quantities by assigning weights to the quantities. Based on the level of importance of the quantities, weights are assigned to the quantities. The below formula for weighted mean includes variables \(x_1\), \(x_2\), \(x_3\)...\(x_n\), and their weights \(w_1\), \(w_2\), \(w_3\)...\(w_n\) respectively. Here this is similar to the average and the weighted mean represents the summary value of all the available quantities. The weighted mean has the same units as that of the individual quantities.
\[ \bar x = \frac{w_1x_1 + w_2x_2 + ......+ w_nx_n}{w_1 + w_2 + ... + w_n} \]
\[\bar x = \frac{\sum w_nx_n}{\sum w_n} \]
Let us look at an example to understand this better.
Example: Find weighted mean for following data set w = {2, 5, 6, 8, 9}, x = {4, 3, 7, 5, 6}
Solution:
Given data sets w = {2, 5, 6, 8, 9}, x = {4, 3, 7, 5, 6} and N = 5
Weighted mean = ∑(weights × quantities) / ∑(weights)
= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5) / (w1 + w2 + w3 + w4 + w5)
= (2 × 4 + 5 × 3 + 6 × 7 + 8 × 5 + 9 × 6) / (2 + 5 + 6 + 8 + 9)
= ( 8 + 15 + 42 + 40 + 54) / 30
= 159 / 30
= 5.3
Therefore, the weighted mean is 5.3.
Weighted Mean Vs Arithmetic Mean
| Weighted Mean | Average Mean |
|---|---|
| The quantities are multiplied with the weighted value, added, and then divided by the weight. | The quantities are all added and divided by the number of observations. |
| It is applied in the daily activities of finance. | It is a mathematical equation. |
| It arrives at a solution to a problem. | It represents a set of data. |
☛Related Articles
Check out the interesting topics to learn more about weighted mean.
Weighted Mean Examples
-
Example 1: A teacher provides the following weightage of 20% for class attendance, 30% for project work, 40% for tests, and 10% for home assignments. A student scores 80/100 for class attendance, 4/5 in project work, 35/50 in tests, and 8/10 in home assignments. Find the final score of the student.
Solution:
\(\begin{align} \bar x &= \frac{w_1x_1 + w_2x_2 + ......+ w_nx_n}{w_1 + w_2 + ... + w_n}
\\&=\frac{20\%.\frac{80}{100} + 30\%.\frac{4}{5} + 40\%.\frac{35}{50} + 10\%.\frac{8}{10}}{20\% + 30\% + 40\% + 10\%} \\&=\frac{20\%.0.8 + 30\%.0.8 + 40\%.0.7 + 10\%.0.8}{100\%} \\&=\frac{0.2 \times 0.8 + 0.3 \times 0.8 + 0.4 \times 0.7 + 0.1 \times 0.8}{1} \\&=0.16 + 0.24 + 0.28 + 0.08 \\&=0.76 \end{align} \)
Therefore, the final score of the student is 0.76. -
Example 2: For a job application 0.8 weightage is given to academic qualification, 0.7 is given to personality, 0.4 is given to the location. The prospective candidate scores 4.5/5 for academic qualification, 3/5 for personality, and 2.8/5 for location. Find the final score received by the candidate.
Solution:
\(\begin{align} \bar x &= \frac{w_1x_1 + w_2x_2 + ......+ w_nx_n}{w_1 + w_2 + ... + w_n}
\\&=\frac{0.8 \times \frac{4.5}{5}+ 0.7 \times \frac{3}{5} + 0.4 \times \frac{2.8}{5}}{0.8 + 0.7 + 0.4} \\&=\frac{0.8 \times 0.9 + 0.7 \times 0.6 + 0.4 \times 0.56}{0.19} \\&=\frac{0.72 + 0.42 + 0.224}{0.19} \\&=\frac{1.364}{0.19} \\&= 7.18 \end{align} \)
Hence, the final score of the candidate is 7.18. -
Example 3: Ben is a fruit merchant who sells various types of fruits in Chicago. Some fruits are of higher quality and are sold at a higher price. He wants you to calculate the weighted mean from the following data:
Grade Unit Sold Unit Price A 100 80 B 50 70 C 20 60 D 15 50 Solution:
\(\begin{align} \bar x &= \frac{w_1x_1 + w_2x_2 + ......+ w_nx_n}{w_1 + w_2 + ... + w_n}
= 100 × 80 + 50 × 70 + 20 × 60 + 15 × 50 / 100 + 50 + 20 + 15
= 8000 + 3500 + 1200 + 750 / 185
= 13450/185
= 75.70
Therefore, the weighted mean is 75.7

FAQs on Weighted Mean
What is the Meaning of Weighted Mean?
The weighted mean is a mean that is calculated by multiplying the weight associated with a particular event or outcome with its associated quantitative outcome and then summing all the products together.
How Do You Calculate Weighted Mean?
Weighted mean can be calculated in two ways.
- When the weights add to 1 then multiply the weights with the value and add them.
- When the weights add to more than 1 then we use the weighted mean formula.
What is the Weighted Mean Formula?
The weighted mean formula is:
\[ \bar x = \frac{w_1x_1 + w_2x_2 + ......+ w_nx_n}{w_1 + w_2 + ... + w_n} \]
\[\bar x = \frac{\sum w_nx_n}{\sum w_n} \]
Where,
- \(x_1\), \(x_2\), \(x_3\)...\(x_n\) are the variables.
- \(w_1\), \(w_2\), \(w_3\)...\(w_n\) are the weights.
When Should I Use Weighted Mean?
When some values weigh more than the other values i.e. count more, that's when weighted mean is used.
visual curriculum