Pascal's Triangle
Pascals triangle or Pascal's triangle is an arrangement of binomial coefficients in triangular form. It is named after the French mathematician Blaise Pascal. The numbers in Pascal's triangle are placed in such a way that each number is the sum of two numbers just above the number. Pascals triangle is used widely in probability theory, combinatorics, and algebra.
Generally, we can use Pascal's triangle to find the coefficients of binomial expansion, to find the probability of heads and tails in a toss, in combinations of certain things, etc. Let us discuss Pascals triangle in detail in the following section.
What is Pascal's Triangle?
A pascal's triangle is an arrangement of numbers in a triangular array such that the numbers at the end of each row are 1 and the remaining numbers are the sum of the nearest two numbers in the above row. This concept is used widely in probability, combinatorics, and algebra. Pascal's triangle is used to find the likelihood of the outcome of the toss of a coin, coefficients of binomial expansions in probability, etc.
Pascals Triangle Explained
Pascals triangle or Pascal's triangle is a special triangle that is named after Blaise Pascal, in this triangle, we start with 1 at the top, then 1s at both sides of the triangle until the end. The middle numbers are so filled that each number is the sum of the two numbers just above it. The number of elements in the nth row is equal to (n + 1) elements. Pascal's triangle can be constructed by writing 1 as the first and the last element of a row and the other elements of the row are obtained from the sum of the two consecutive elements of the previous row. Pascal's triangle can be constructed easily by just adding the pair of successive numbers in the preceding lines and writing them in the new line.
Pascals triangle or Pascal's triangle is shown in the image below. Here, we can see that any number is the sum of the two numbers just above that number.

Pascal's Triangle Formula
The formula to fill the number in the nth column and mth row of Pascal's triangle we use the Pascals triangle formula. The formula requires the knowledge of the elements in the (n-1)th row, and (m-1)th and nth columns. The elements of the nth row of Pascal's triangle are given by, nC0, nC1, nC2, ..., nCn. The formula for Pascal's triangle is:
nCm = n-1Cm-1 + n-1Cm
where
- nCm represents the (m+1)th element in the nth row.
- n is a non-negative integer, and
- 0 ≤ m ≤ n.
Let us understand this with an example. If we want to find the 3rd element in the 4th row, this means we want to calculate 4C2. Then according to the formula, we get
4C2 = 4-1C2-1 + 4-1C2
⇒ 4C2 = 3C1 + 3C2
So, this means we need to add the 2nd element in the 3rd row (i.e. 3) with the 3rd element in the 3rd row (i.e. 3.). So our answer will be 4C2 = 3 + 3 = 6
Pascal's Triangle Binomial Expansion
Pascals triangle can also be used to find the coefficient of the terms in the binomial expansion. Pascal's triangle is a handy tool to quickly verify if the binomial expansion of the given polynomial is done correctly or not. Let us understand this with an example

We know the expansion of (x+y)2 is x2 + 2xy + y2. If we write all the hidden terms and coefficient of this expansion, we can write that x2 + 2xy + y2 = 1x2 y0+ 2x1y1 + 1x0y2. And now if we check the elements in the second row of the Pascals triangle, we will find the numbers 1 2 1. This is the exact match of the coefficients of the terms in the expansion of (x+y)2. Now if we take the binomial expansion of the polynomial (x+y)n, we have the following expression.
(x+y)n = a0 xn y0+ a1 xn-1 y1 + a2 xn-2 y2 + ... + an x0 yn
We can get the am by using the binomial formula nCm = n-1Cm-1 + n-1Cm
Pascals Triangle Probability
Pascal's triangle can be used in various places in the field of mathematics. Pascal's triangle is used in probability, can be used to find the number of combinations, etc. It gives us the number of combinations of heads or tails that are possible from the number of tosses. For example, if we toss a coin two times, we get 1 time HH, 2 times HT or TH, and 1 time TT, which is the exact match of the elements in the second row of the Pascals triangle. Similarly, we get the following results in the various number of tosses:
|
Number of Tosses or Row of Pascals Triangle |
Outcomes in Combinations | Elements in Pascals Triangle |
|---|---|---|
| 1 | {H} {T} |
1, 1 |
| 2 | {HH} {HT TH} {TT} |
1, 2, 1 |
| 3 | {HHH} {HHT, HTH, THH} {HTT, THT, TTH} {TTT} |
1, 3, 3, 1 |
| 4 | {HHHH} {HHHT, HHTH, HTHH, THHH} {HHTT, HTHT, HTTH, THHT, THTH, TTHH} {HTTT, THTT, TTHT, TTTH} {TTTT} |
1, 4, 6, 4, 1 |
| ...etc... | ... etc ... | etc... |
Pascal's Triangle Pattern
Pascal's triangle has various patterns within the triangle which were found and explained by Pascal himself or were known way before him. A few of the Pascal triangle patterns are:
-
The sum of values in the nth row is 2n. For example, in the 4th row 1 4 6 4 1, sum of the elements is 1 + 4 + 6 + 4 + 1 = 16 = 24.
-
If a row has the second element a prime number, then all the following elements in the row are divisible by that prime number (not considering 1s). ex. 1 5 10 10 5 1.
- By adding the different diagonal elements of Pascal's triangle, we get the Fibonacci series.

- Few more patterns on the diagonal of a Pascal's triangle can be seen in the following image:
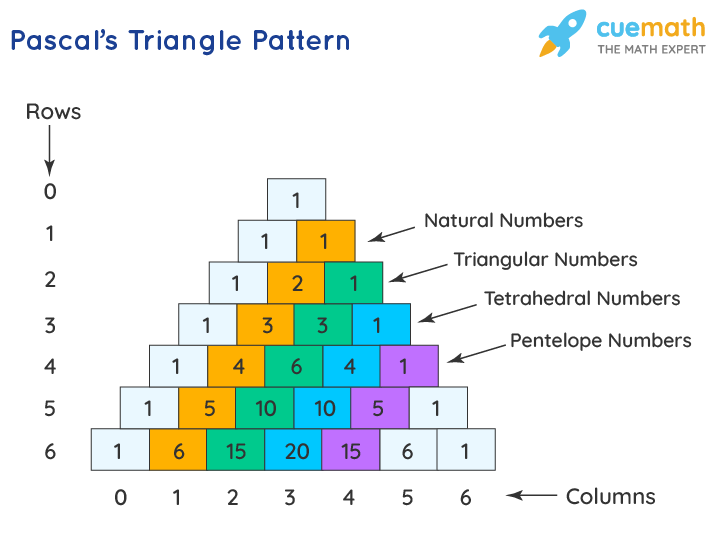
Important Notes on Pascal's Triangle:
- The elements in the Pascals triangle can find out by finding the sum of the two adjoint elements in the preceding row.
- The sum of values in the nth row is 2n.
- Pascal's triangle is used to determine the coefficients of binomial expansions.
Related Topics:
Pascal's Triangle Examples
-
Example 1: A coin is tossed three times, find the probability of getting exactly 2 tails.
Solution:
Using the Pascal triangle formula, the total number of outcomes will be 23 = 8 (1 + 3 + 3 + 1 = 8 )
Where 3 of them give exactly two tails.
So the probability of getting exactly two tails is 3/8, or 37.5%
Answer: The probability of getting exactly two tails is 37.5%
-
Example 2: Find all the coefficients of the expansion of the polynomial (x + y)6 using the Pascals triangle.
Solution:
According to the Pascals triangle, the coefficients of the expansion of the (x + y)6 will be the elements in row 6 of the Pascals triangle.

Elements in the 6th row of the Pascals triangle are 1, 6, 15, 20, 15, 6, 1.
Answer: The coefficients of the expansion of (x + y)6 are 1, 6, 15, 20, 15, 6, 1.
-
Example 3: Find the sum of the elements in the 20th row of the Pascals triangle.
Solution:
Using the Pascals triangle formula for the sum of the elements in the nth row of the Pascals triangle:
Sum = 2n where n is the number of the row.
Hence Sum = 220
Sum = 1048576
Answer: The sum of the elements in the 20th row is 1048576.

FAQs on Pascal's Triangle
What is Pascal's Triangle?
A pascal's triangle is an arrangement of numbers in a triangular array such that the numbers at the end of each row are 1 and the remaining numbers are the sum of the nearest two numbers in the above row.
What is Pascal's Triangle Used For?
Pascals triangle can be used for various purposes in mathematics. It is used in the binomial expansion of a polynomial, in probability, to find the number of combinations, and can be used to find the Fibonacci series. Pascal's triangle is a very useful tool and has various properties that can be useful in various aspects of mathematics.
What is The Rule for Pascal's Triangle?
The rule that Pascal's triangle has is that we start with 1 at the top, then 1s at both sides of the triangle until the end. The middle numbers, each is the sum of the two consecutive numbers just above it. Hence to construct a Pascal's triangle we just need to add the two numbers just above the number.
What are 3 Patterns In Pascal's Triangle?
The three patterns in the Pascals triangle are:
-
The sum of values in the nth row is 2n. For. example we have the values in the 4th row 1 4 6 4 1, and the sum of these elements is 1 + 4 + 6 + 4 + 1 = 16 = 24.
-
If a row has the second element which is a prime number, then all the following elements in the row are divisible by that prime number(not considering 1s), for. ex. 1 5 10 10 5 1.
- By adding the different diagonals elements of a Pascals triangle, we get the Fibonacci series.
How Do You Use Pascal's Triangle in Binomial Expansion?
Pascals triangle can also be used to find the coefficient of the terms in the binomial expansion. Let us understand this with an example. We know the expansion of (x+y)2 is x2 + 2xy + y2 If we write all the hidden terms and coefficient of this expansion, we can write that x2 + 2xy + y2 = 1x2 y0+ 2x1y1 + 1x0y2, and now if we check the elements in the second row of the Pascals triangle we will find the numbers 1 2 1. Hence if we want to find the coefficients in the binomial expansion, we use Pascals triangle.
What is Pascal's Triangle Formula?
Pascal's formula is used to find the element in the Pascal triangle. The formula for Pascal's triangle is nCm = n-1Cm-1 + n-1Cm
where
- nCm represents the (m+1)th element in the nth row.
- n is a non-negative integer, and
- 0 ≤ m ≤ n.
What is the 5th Row of Pascal's Triangle?
There are 6 elements in the 5th row of the pascal triangle. The 5th row in Pascal's triangle is 1 5 10 10 5 1. The sum of the elements in the 5th row of the Pascals triangle is 32 which can also be verified by 25 = 32.
What is the First Element in Each Row of Pascal's Triangle?
The first element in each row of Pascal's triangle is 1. This term is referred to as the 0th term of each row.
visual curriculum